Actor Partner Interdependence Model With Multilevel Analysis

Last updated on Jan 5, 2023 11 min read Statistics

Every time I teach multilevel modeling (MLM) at USC, I have students interested in running the actor partner independence model (APIM) using dyadic model. While such models are easier to fit with structural equation modeling, it can also be fit using MLM. In this post I provide a software tutorial for fitting such a model using MLM, and contrast to results to SEM.

Note that this is not a conceptual introduction to APIM. Please check out this chapter and this paper.

There is also this great tutorial on using the nlme package, which uses the dummy variable trick to allow a univariate MLM to handle multivariate analyses. The current blog post is similar but with a different package.

See also https://hydra.smith.edu/~rgarcia/workshop/Day_1-Actor-Partner_Interdependence_Model.html with the same example using nlme::gls().

Load Packages

library(tidyverse)
library(psych)
library(glmmTMB)

Data

The data set comes from https://github.com/RandiLGarcia/dyadr/tree/master/data, which has 148 married couples. You can see the codebook at https://randilgarcia.github.io/week-dyad-workshop/Acitelli%20Codebook.pdf

pair_data <- here::here("data_files", "acipair.RData")
# Download data if not already exists in local folder
if (!file.exists(pair_data)) {
  download.file("https://github.com/RandiLGarcia/dyadr/raw/master/data/acipair.RData",
                pair_data)
}
load(pair_data)
# Show data
head(acipair)
##   CoupleID  Yearsmar Partnum Gender_A SelfPos_A OtherPos_A Satisfaction_A
## 1        3  8.202667       1     Wife       4.8        4.6       4.000000
## 2        3  8.202667       2  Husband       3.8        4.0       3.666667
## 3       10 10.452667       1     Wife       4.6        3.8       3.166667
## 4       10 10.452667       2  Husband       4.2        4.0       3.666667
## 5       11 -8.297333       1     Wife       5.0        4.4       3.833333
## 6       11 -8.297333       2  Husband       4.2        4.8       3.833333
##   Tension_A SimHob_A Gender_P SelfPos_P OtherPos_P Satisfaction_P Tension_P
## 1       1.5        0     MALE       3.8        4.0       3.666667       2.5
## 2       2.5        1   FEMALE       4.8        4.6       4.000000       1.5
## 3       4.0        0     MALE       4.2        4.0       3.666667       2.0
## 4       2.0        0   FEMALE       4.6        3.8       3.166667       4.0
## 5       2.5        0     MALE       4.2        4.8       3.833333       2.5
## 6       2.5        0   FEMALE       5.0        4.4       3.833333       2.5
##   SimHob_P                   Gender COtherPos_A COtherPos_P CTension_A
## 1        1 Wife                          0.3365     -0.2635    -0.9307
## 2        0 Husband                      -0.2635      0.3365     0.0693
## 3        0 Wife                         -0.4635     -0.2635     1.5693
## 4        0 Husband                      -0.2635     -0.4635    -0.4307
## 5        0 Wife                          0.1365      0.5365     0.0693
## 6        0 Husband                       0.5365      0.1365     0.0693
##   CTension_P
## 1     0.0693
## 2    -0.9307
## 3    -0.4307
## 4     1.5693
## 5     0.0693
## 6     0.0693

Hypothetical Research Question

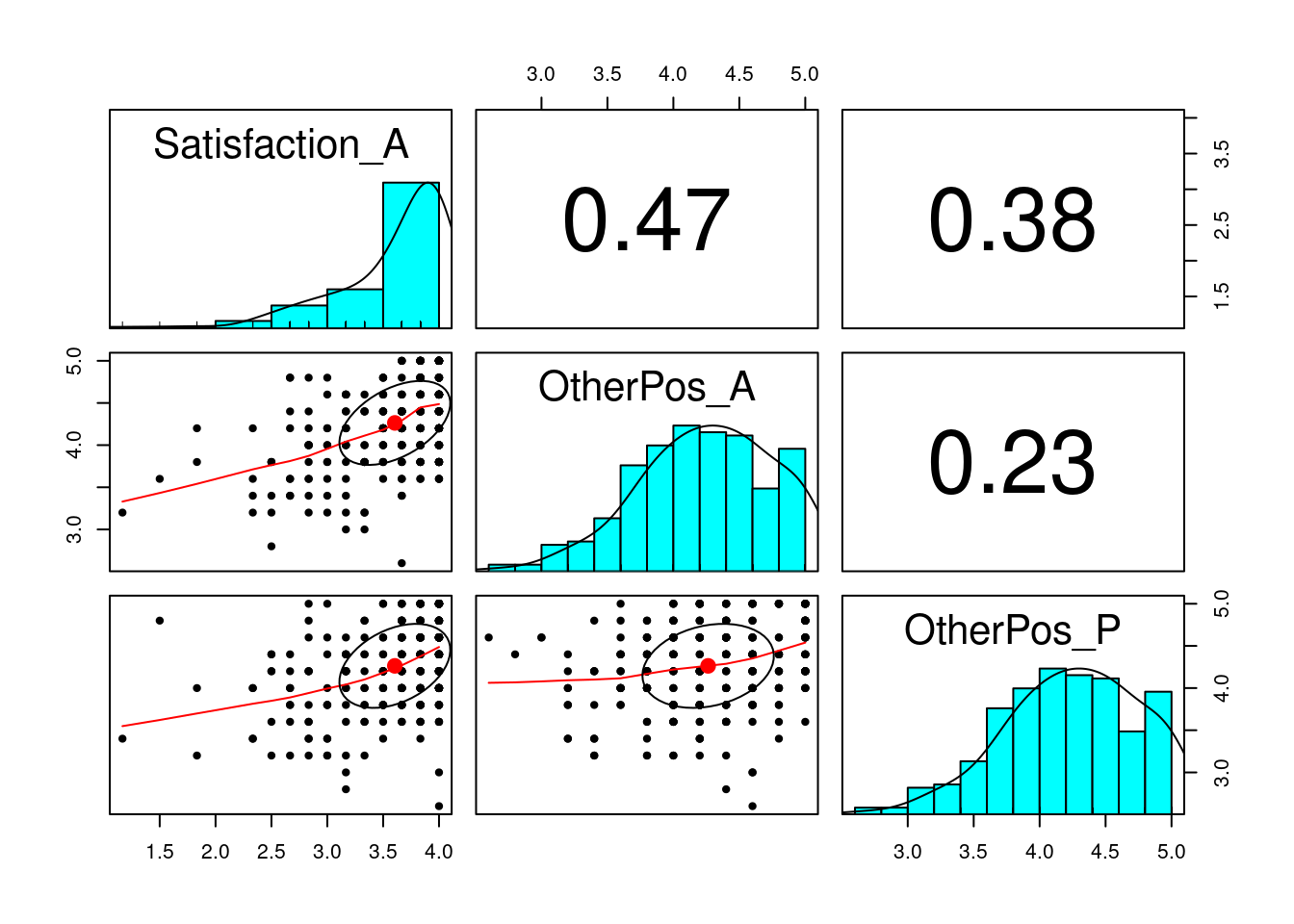
Here we have a hypothetical research question of how a person views their partners (OtherPos_A) and how their partner views them (OtherPos_P) predict their marriage satisfaction (Satisfaction_A).

# Overall
pairs.panels(
  subset(acipair, select = c("Satisfaction_A", "OtherPos_A", "OtherPos_P"))
)

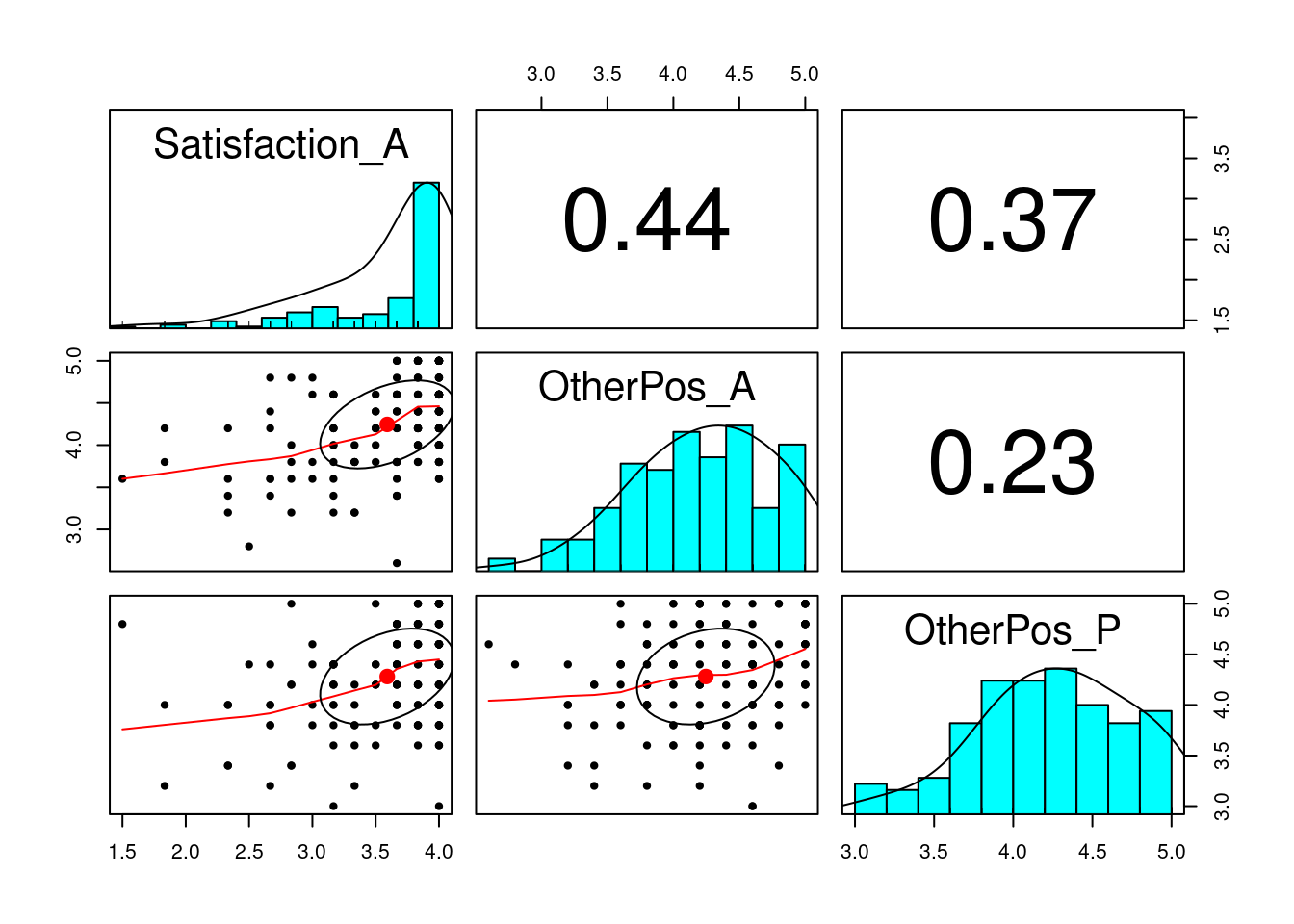
# Wife
pairs.panels(
  subset(acipair, subset = Gender_A == "Wife",
         select = c("Satisfaction_A", "OtherPos_A", "OtherPos_P"))
)

# Husband
pairs.panels(
  subset(acipair, subset = Gender_A == "Husband",
         select = c("Satisfaction_A", "OtherPos_A", "OtherPos_P"))
)

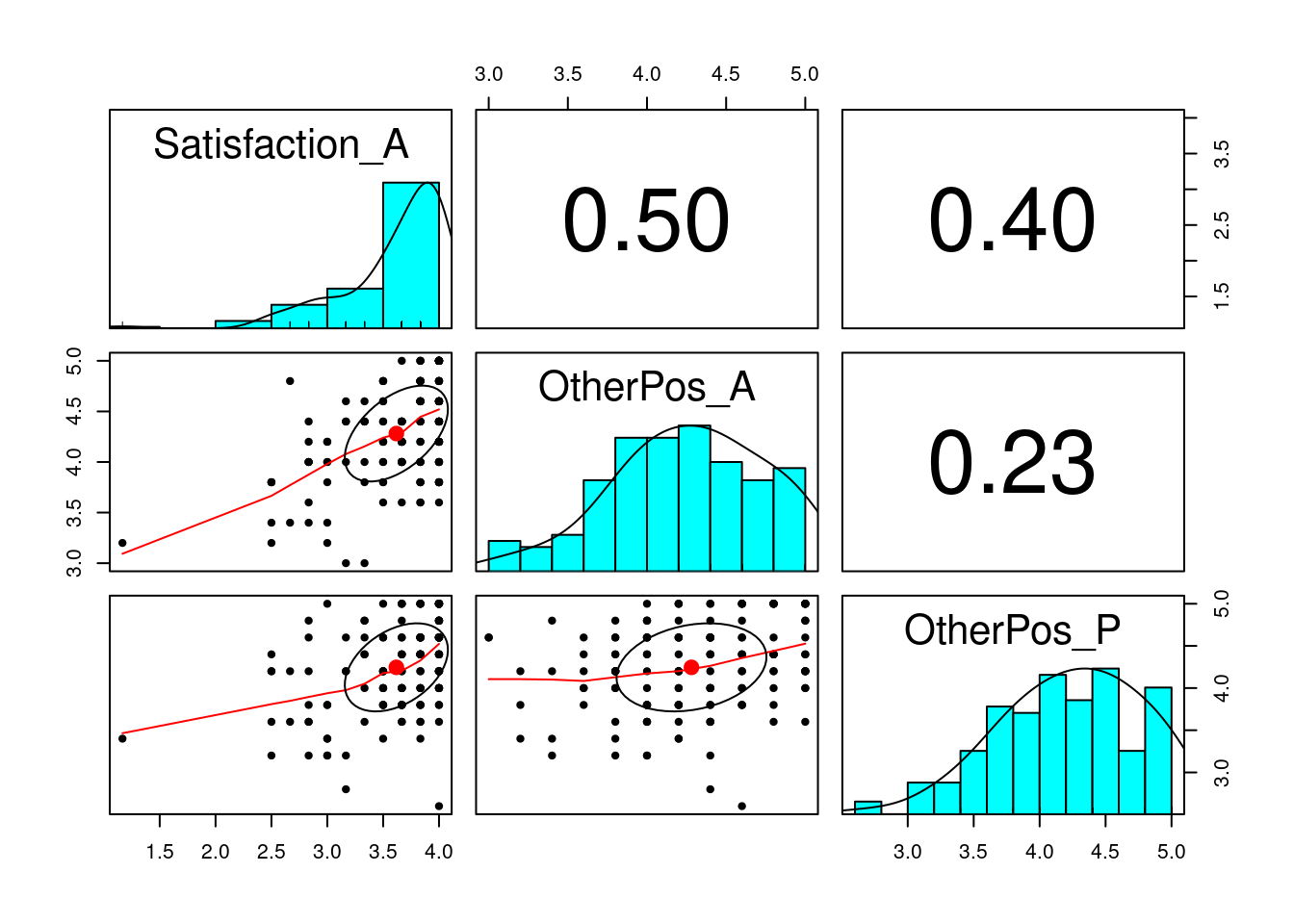
# Note the ceiling effect of satisfaction

In this example, there are two major paths of interest:

  • Actor effect: OtherPos_A to Satisfaction_A
  • Partner effect: OtherPos_P to Satisfaction_A

In addition, for distinguishable dyads, like husband and wives, we want the gender interactions as well, resulting in four paths of interest (actor/partner effects for husbands/wives).

Distinguishable Dyads

Level 1:

\[ \begin{aligned} \text{Satisfaction}_{ij} & = \beta_{0j} + \beta_{1j} \text{View Partner}_{ij} + \beta_{2j} \text{Partner View}_{ij} + \beta_{3j} \text{Gender}_{ij} \\ & \quad + \beta_{4j} \text{View Partner}_{ij} \times \text{Gender}_{ij} \\ & \quad + \beta_{5j} \text{Partner View}_{ij} \times \text{Gender}_{ij} + e_{ij} \\ e_{ij} & \sim N(0, \sigma^2_{ij}) \\ \log(\sigma^2_{ij}) & = \beta^{s}_{0j} + \beta^{s}_{1j} \text{Gender}_{ij} \end{aligned} \]

Level 2:

\[ \begin{aligned} \beta_{0j} & = \gamma_{00} + u_{0j} \\ \beta_{1j} & = \gamma_{10} \\ \beta_{2j} & = \gamma_{20} \\ \beta_{3j} & = \gamma_{30} \\ \beta_{4j} & = \gamma_{40} \\ \beta_{5j} & = \gamma_{50} \\ \beta^{s}_{0j} & = \gamma^{s}_{00} \\ \beta^{s}_{1j} & = \gamma^{s}_{10} \\ u_{0j} | \text{Wife} & \sim N(0, \tau^2_{0 | H}) \\ u_{1j} | \text{Husband} & \sim N(0, \tau^2_{0 | W}) \end{aligned} \] Note that the variance components are allowed to be different across genders.

m_apim <- glmmTMB(
  Satisfaction_A ~ (OtherPos_A + OtherPos_P) * Gender_A +
    us(0 + Gender_A | CoupleID),
  dispformula = ~ Gender_A,
  data = acipair,
  REML = FALSE
)
summary(m_apim)
##  Family: gaussian  ( identity )
## Formula:          
## Satisfaction_A ~ (OtherPos_A + OtherPos_P) * Gender_A + us(0 +  
##     Gender_A | CoupleID)
## Dispersion:                      ~Gender_A
## Data: acipair
## 
##      AIC      BIC   logLik deviance df.resid 
##    297.6    338.2   -137.8    275.6      285 
## 
## Random effects:
## 
## Conditional model:
##  Groups   Name            Variance Std.Dev. Corr 
##  CoupleID Gender_AWife    0.08734  0.2955        
##           Gender_AHusband 0.07716  0.2778   0.98 
##  Residual                      NA      NA        
## Number of obs: 296, groups:  CoupleID, 148
## 
## Conditional model:
##                            Estimate Std. Error z value Pr(>|z|)    
## (Intercept)                 0.61125    0.40861   1.496    0.135    
## OtherPos_A                  0.37770    0.07317   5.162 2.44e-07 ***
## OtherPos_P                  0.32148    0.08069   3.984 6.78e-05 ***
## Gender_AHusband             0.07921    0.38779   0.204    0.838    
## OtherPos_A:Gender_AHusband  0.04669    0.10458   0.446    0.655    
## OtherPos_P:Gender_AHusband -0.05983    0.10628  -0.563    0.573    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Dispersion model:
##                 Estimate Std. Error z value Pr(>|z|)
## (Intercept)      -2.1549   262.4017  -0.008    0.993
## Gender_AHusband  -0.6085   680.1472  -0.001    0.999

The model results show:

  • Actor effect for Wife: 0.37 (SE = 0.07)
  • Partner effect for Wife: 0.32 (SE = 0.08)
  • Difference of actor effect (Husband - Wife): 0.05 (SE = 0.10)
  • Difference of partner effect (Husband - Wife): -0.06 (SE = 0.11)
  • Gender difference (Husband - Wife) when Partner View is 0: 0.08 (SE = 0.39)

We can also estimate the actor and partner effects for both Husband and Wife by suppressing the intercept:

m_apim2 <- glmmTMB(
  Satisfaction_A ~ 0 + Gender_A + (OtherPos_A + OtherPos_P):Gender_A +
    us(0 + Gender_A | CoupleID),
  dispformula = ~ Gender_A,
  data = acipair,
  REML = FALSE,
  # The default optimizer did not converge; try optim
  control = glmmTMBControl(
    optimizer = optim,
    optArgs = list(method = "BFGS")
  )
)
summary(m_apim2)
##  Family: gaussian  ( identity )
## Formula:          
## Satisfaction_A ~ 0 + Gender_A + (OtherPos_A + OtherPos_P):Gender_A +  
##     us(0 + Gender_A | CoupleID)
## Dispersion:                      ~Gender_A
## Data: acipair
## 
##      AIC      BIC   logLik deviance df.resid 
##    297.6    338.2   -137.8    275.6      285 
## 
## Random effects:
## 
## Conditional model:
##  Groups   Name            Variance Std.Dev. Corr 
##  CoupleID Gender_AWife    0.11075  0.3328        
##           Gender_AHusband 0.05813  0.2411   1.00 
##  Residual                      NA      NA        
## Number of obs: 296, groups:  CoupleID, 148
## 
## Conditional model:
##                            Estimate Std. Error z value Pr(>|z|)    
## Gender_AWife                0.61125    0.40861   1.496   0.1347    
## Gender_AHusband             0.69046    0.33941   2.034   0.0419 *  
## Gender_AWife:OtherPos_A     0.37770    0.07317   5.162 2.44e-07 ***
## Gender_AHusband:OtherPos_A  0.42439    0.06703   6.332 2.43e-10 ***
## Gender_AWife:OtherPos_P     0.32148    0.08069   3.984 6.78e-05 ***
## Gender_AHusband:OtherPos_P  0.26165    0.06078   4.305 1.67e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Dispersion model:
##                 Estimate Std. Error z value Pr(>|z|)
## (Intercept)      -2.3805    94.5039  -0.025    0.980
## Gender_AHusband  -0.1192   150.4151  -0.001    0.999

Indistinguishable Dyads

As the interaction terms were not significant, one may want to remove them. Similarly, the variance components did not look too different across genders, so we may make them equal as well:

m2 <- glmmTMB(
  Satisfaction_A ~ Gender_A + OtherPos_A + OtherPos_P + (1 | CoupleID),
  dispformula = ~ 1,
  data = acipair,
  REML = FALSE
)
summary(m2)
##  Family: gaussian  ( identity )
## Formula:          
## Satisfaction_A ~ Gender_A + OtherPos_A + OtherPos_P + (1 | CoupleID)
## Data: acipair
## 
##      AIC      BIC   logLik deviance df.resid 
##    294.5    316.6   -141.2    282.5      290 
## 
## Random effects:
## 
## Conditional model:
##  Groups   Name        Variance Std.Dev.
##  CoupleID (Intercept) 0.08047  0.2837  
##  Residual             0.09155  0.3026  
## Number of obs: 296, groups:  CoupleID, 148
## 
## Dispersion estimate for gaussian family (sigma^2): 0.0915 
## 
## Conditional model:
##                 Estimate Std. Error z value Pr(>|z|)    
## (Intercept)      0.65818    0.32074   2.052   0.0402 *  
## Gender_AHusband  0.02315    0.03523   0.657   0.5111    
## OtherPos_A       0.39935    0.04706   8.487  < 2e-16 ***
## OtherPos_P       0.28904    0.04706   6.143 8.12e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Finally, we may also remove the main effect for Gender:

m3 <- glmmTMB(
  Satisfaction_A ~ OtherPos_A + OtherPos_P + (1 | CoupleID),
  dispformula = ~ 1,
  data = acipair,
  REML = FALSE
)
summary(m3)
##  Family: gaussian  ( identity )
## Formula:          Satisfaction_A ~ OtherPos_A + OtherPos_P + (1 | CoupleID)
## Data: acipair
## 
##      AIC      BIC   logLik deviance df.resid 
##    292.9    311.3   -141.4    282.9      291 
## 
## Random effects:
## 
## Conditional model:
##  Groups   Name        Variance Std.Dev.
##  CoupleID (Intercept) 0.08034  0.2834  
##  Residual             0.09181  0.3030  
## Number of obs: 296, groups:  CoupleID, 148
## 
## Dispersion estimate for gaussian family (sigma^2): 0.0918 
## 
## Conditional model:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  0.66975    0.32025   2.091   0.0365 *  
## OtherPos_A   0.40042    0.04705   8.510  < 2e-16 ***
## OtherPos_P   0.28797    0.04705   6.120 9.34e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Model Comparison

anova(m_apim, m2, m3)
## Data: acipair
## Models:
## m3: Satisfaction_A ~ OtherPos_A + OtherPos_P + (1 | CoupleID), zi=~0, disp=~1
## m2: Satisfaction_A ~ Gender_A + OtherPos_A + OtherPos_P + (1 | CoupleID), zi=~0, disp=~1
## m_apim: Satisfaction_A ~ (OtherPos_A + OtherPos_P) * Gender_A + us(0 + , zi=~0, disp=~Gender_A
## m_apim:     Gender_A | CoupleID), zi=~0, disp=~1
##        Df    AIC    BIC  logLik deviance  Chisq Chi Df Pr(>Chisq)
## m3      5 292.88 311.34 -141.44   282.88                         
## m2      6 294.45 316.60 -141.23   282.45 0.4312      1     0.5114
## m_apim 11 297.61 338.20 -137.80   275.61 6.8458      5     0.2324

There model with all paths equal is the best in terms of AIC and BIC, and the likelihood ratio tests were not significant.

Using SEM

Distinguishable Dyads

# Wide format
aciwide <- filter(acipair, Partnum == 1)  # Actor = Wife; Partner = Husband
library(lavaan)
## This is lavaan 0.6-11
## lavaan is FREE software! Please report any bugs.
## 
## Attaching package: 'lavaan'
## The following object is masked from 'package:psych':
## 
##     cor2cov
apim_mod <- ' Satisfaction_A + Satisfaction_P ~ OtherPos_A + OtherPos_P '
apim_fit <- sem(apim_mod, data = aciwide)
summary(apim_fit)
## lavaan 0.6-11 ended normally after 12 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                         7
##                                                       
##   Number of observations                           148
##                                                       
## Model Test User Model:
##                                                       
##   Test statistic                                 0.000
##   Degrees of freedom                                 0
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Regressions:
##                    Estimate  Std.Err  z-value  P(>|z|)
##   Satisfaction_A ~                                    
##     OtherPos_A        0.378    0.073    5.162    0.000
##     OtherPos_P        0.321    0.081    3.984    0.000
##   Satisfaction_P ~                                    
##     OtherPos_A        0.262    0.061    4.305    0.000
##     OtherPos_P        0.424    0.067    6.332    0.000
## 
## Covariances:
##                     Estimate  Std.Err  z-value  P(>|z|)
##  .Satisfaction_A ~~                                    
##    .Satisfaction_P     0.080    0.015    5.221    0.000
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)
##    .Satisfaction_A    0.203    0.024    8.602    0.000
##    .Satisfaction_P    0.140    0.016    8.602    0.000
library(semPlot)
library(semptools)
p1 <- semPaths(apim_fit, what = "est", 
               rotation = 2, 
               sizeMan = 15,
               nCharNodes = 0,
               edge.label.cex = 1.15,
               label.cex = 1.25)
my_label_list <- list(list(node = "Satisfaction_A", to = "Satisfaction (W)"),
                      list(node = "Satisfaction_P", to = "Satisfaction (H)"),
                      list(node = "OtherPos_A", to = "View\nPartner (W)"),
                      list(node = "OtherPos_P", to = "View\nPartner (H)"))
p2 <- change_node_label(p1, my_label_list)
p3 <- mark_se(p2, apim_fit, sep = "\n")
my_position_list <- c("Satisfaction_A ~ OtherPos_P" = .25,
                      "Satisfaction_P ~ OtherPos_A" = .25)
p4 <- set_edge_label_position(p3, my_position_list)
plot(p4)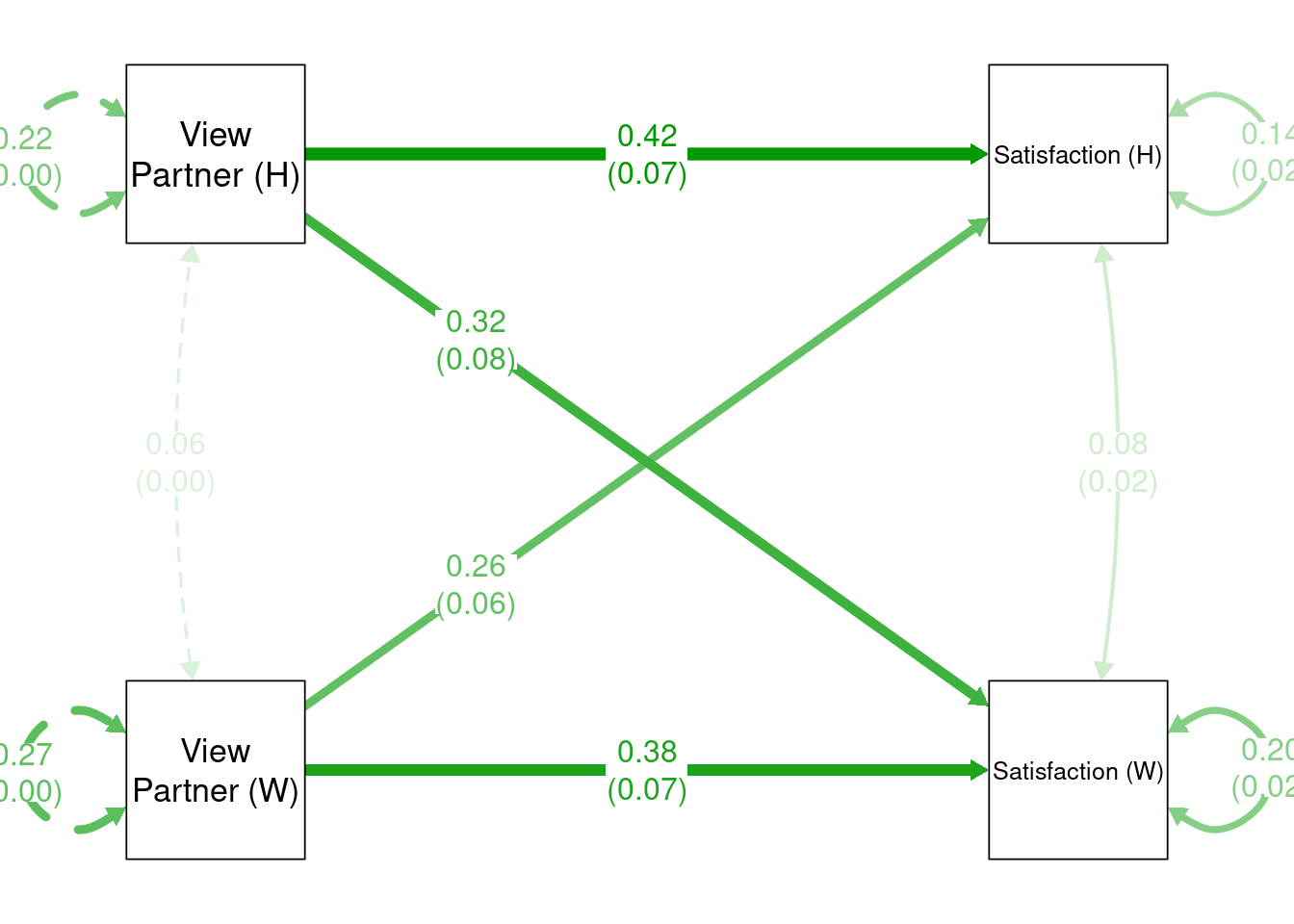

Indistinguishable Dyads

apim2_mod <- ' Satisfaction_A ~ a * OtherPos_A + p * OtherPos_P
               Satisfaction_P ~ p * OtherPos_A + a * OtherPos_P 
               # Constrain the variances and means to be equal
               Satisfaction_A ~~ v * Satisfaction_A
               Satisfaction_P ~~ v * Satisfaction_P
               Satisfaction_A ~ m * 1
               Satisfaction_P ~ m * 1 '
apim2_fit <- sem(apim2_mod, data = aciwide)
summary(apim2_fit)
## lavaan 0.6-11 ended normally after 22 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                         9
##   Number of equality constraints                     4
##                                                       
##   Number of observations                           148
##                                                       
## Model Test User Model:
##                                                       
##   Test statistic                                 7.277
##   Degrees of freedom                                 4
##   P-value (Chi-square)                           0.122
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Regressions:
##                    Estimate  Std.Err  z-value  P(>|z|)
##   Satisfaction_A ~                                    
##     OtherPos_A (a)    0.400    0.047    8.510    0.000
##     OtherPos_P (p)    0.288    0.047    6.120    0.000
##   Satisfaction_P ~                                    
##     OtherPos_A (p)    0.288    0.047    6.120    0.000
##     OtherPos_P (a)    0.400    0.047    8.510    0.000
## 
## Covariances:
##                     Estimate  Std.Err  z-value  P(>|z|)
##  .Satisfaction_A ~~                                    
##    .Satisfaction_P     0.080    0.016    5.145    0.000
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)
##    .Satsfctn_A (m)    0.670    0.320    2.091    0.036
##    .Satsfctn_P (m)    0.670    0.320    2.091    0.036
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)
##    .Satsfctn_A (v)    0.172    0.016   11.024    0.000
##    .Satsfctn_P (v)    0.172    0.016   11.024    0.000
p1 <- semPaths(apim2_fit, what = "est", 
               rotation = 2, 
               sizeMan = 15,
               nCharNodes = 0,
               edge.label.cex = 1.15,
               label.cex = 1.25,
               intercepts = FALSE)
my_label_list <- list(list(node = "Satisfaction_A", to = "Satisfaction (W)"),
                      list(node = "Satisfaction_P", to = "Satisfaction (H)"),
                      list(node = "OtherPos_A", to = "View\nPartner (W)"),
                      list(node = "OtherPos_P", to = "View\nPartner (H)"))
p2 <- change_node_label(p1, my_label_list)
p3 <- mark_se(p2, apim2_fit, sep = "\n")
my_position_list <- c("Satisfaction_A ~ OtherPos_P" = .25,
                      "Satisfaction_P ~ OtherPos_A" = .25)
p4 <- set_edge_label_position(p3, my_position_list)
plot(p4)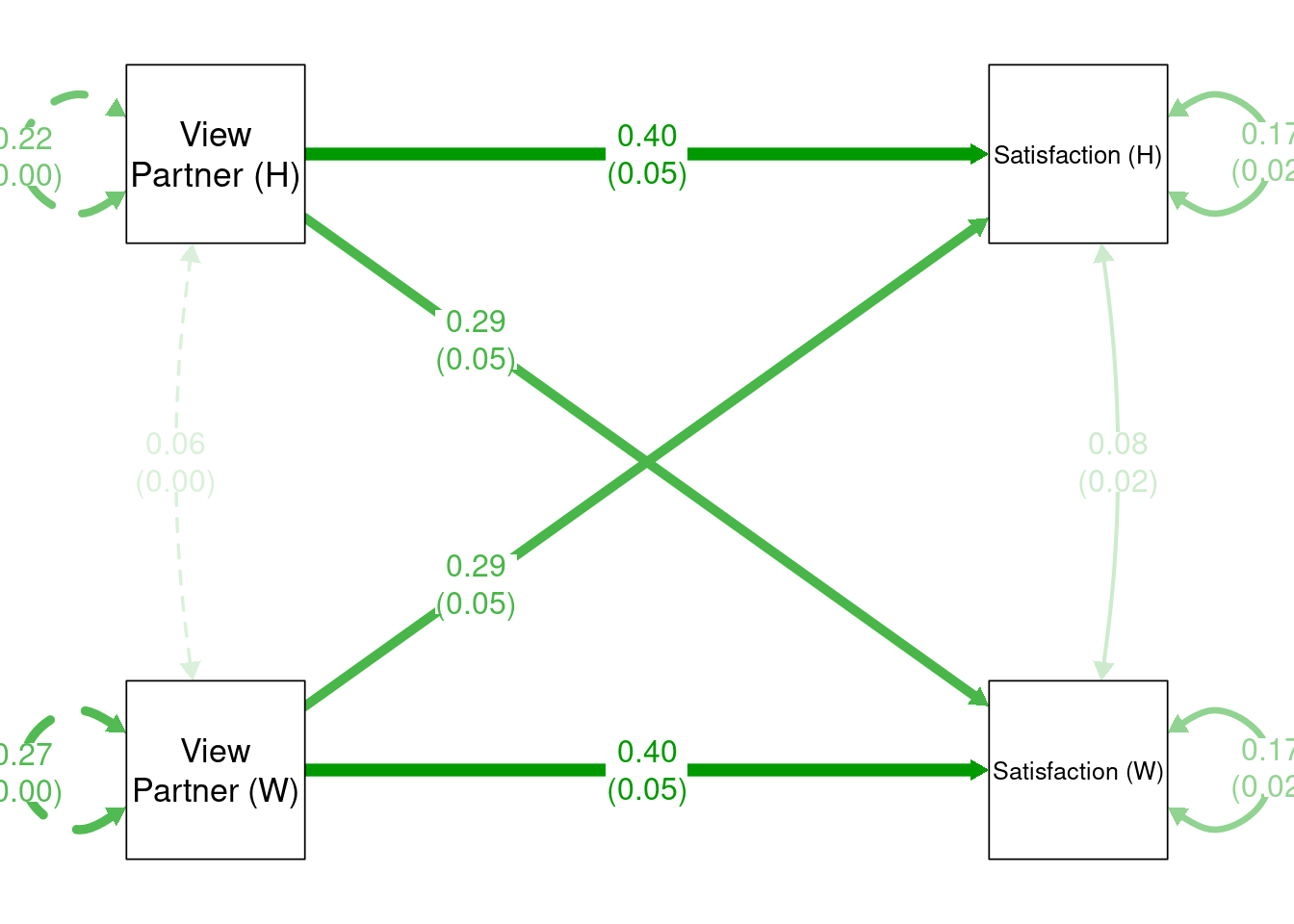

The results are basically identical.

Multilevel
Yuan Bo 袁博
Yuan Bo 袁博
Associate Professor of Psychology (Social Psychology)

My research examines the nature and dynamics of social norms, namely how norms may emerge and become stable, why norms may suddenly change, how is it possible that inefficient or unpopular norms survive, and what motivates people to obey norms. I combines laboratory and simulation experiments to test theoretical predictions and build empirically-grounded models of social norms and their dynamics.

comments powered by Disqus

Related