Multilevel Modeling

# Multilevel Modeling
## Introduction and Recent Advances for Behavioral Research
<html>
<div style="float:left">

</div>
<hr color='#EB811B' size=1px width=796px>
</html>
### Mark Lai
### 2018/12/04

---

# Different Names

Hierarchical linear model .font60[(HLM; Raudenbush and Bryk, 2002)]

Mixed/Mixed-effects model .font60[(Littell, Milliken, Stroup, and Wolfinger, 1996)]

Random coefficient model .font60[(de Leeuw and Kreft, 1986)]

Variance component model .font60[(Aitkin and Longford, 1986)]

---

# Roadmap

What are multilevel data?

Why use MLM?
- Avoid underestimated _SE_
- Cluster-specific (or person-specific) regression lines
- Avoid Ecological Fallacy

Recent advances

---

# What Are Multilevel Data?

---

# Multilevel Data

Nested Data
- Students in classrooms/schools
- Siblings in families
- Clients in therapy groups/therapists/clinics
- Employees in organizations in countries

---

# Multilevel Data

- Repeated measures in individuals

### Network Graph

<div id="htmlwidget-442b1382a5ecf7953b03" style="width:100%;height:25%;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-442b1382a5ecf7953b03">{"x":{"diagram":"\ndigraph boxes_and_circles {\n  graph [overlap = true, fontsize = 24]\n\n  node [penwidth = 0, fontname = \"Helvetica\"]\n  # Schools\n  A; B; C; D\n  # Students\n  1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11\n\n  # edges\n  edge [dir = \"none\"]\n  A -> {1; 2; 3}\n  B -> {4; 5}\n  C -> {6; 7; 8; 9}\n  D -> {10; 11}\n}\n","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>

???
Talk about level 1 and level 2

---

---

# Applications of MLM

Psychotherapy
- Heterogeneity of treatment effectiveness across therapists

Educational research
- Teacher expectations on students' performance

Organizational research
- Job strain and ambulatory blood pressure

---

# Applications of MLM (cont'd)

Cross-national/neighborhood research
- Sociopolitical influence on psychological processes (e.g., age and generalized trust)
- Post-materialism, locus of control, and concern for global warming

Longitudinal analysis/repeated measures
- Aging, self-esteem, and stress appraisal

---

# Example Data

Sample simulated data on students' popularity .font60[(Hox, Moerbeek, and Van
de
Schoot, 2018)]
- 2000 pupils (level 1) in 100 classrooms
(level 2)

Main outcome:
- `popular`: popularity teacher evaluation (0 to 10)

---

.font60[
<div id="htmlwidget-58d2e9d9c54198f1dc08" style="width:100%;height:auto;" class="datatables html-widget"></div>
<script type="application/json" data-for="htmlwidget-58d2e9d9c54198f1dc08">{"x":{"filter":"none","data":[["1","2","3","4","5","6","7","8","9","10","11","12","13","14","15","16","17","18","19","20","21","22","23","24","25","26","27","28","29","30","31","32","33","34","35","36","37","38","39","40","41","42","43","44","45","46","47","48","49","50","51","52","53","54","55","56","57","58","59","60","61","62","63","64","65","66","67","68","69","70","71","72","73","74","75","76","77","78","79","80","81","82","83","84","85","86","87","88","89","90","91","92","93","94","95","96","97","98","99","100","101","102","103","104","105","106","107","108","109","110","111","112","113","114","115","116","117","118","119","120","121","122","123","124","125","126","127","128","129","130","131","132","133","134","135","136","137","138","139","140","141","142","143","144","145","146","147","148","149","150","151","152","153","154","155","156","157","158","159","160","161","162","163","164","165","166","167","168","169","170","171","172","173","174","175","176","177","178","179","180","181","182","183","184","185","186","187","188","189","190","191","192","193","194","195","196","197","198","199","200","201","202","203","204","205","206","207","208","209","210","211","212","213","214","215","216","217","218","219","220","221","222","223","224","225","226","227","228","229","230","231","232","233","234","235","236","237","238","239","240","241","242","243","244","245","246","247","248","249","250","251","252","253","254","255","256","257","258","259","260","261","262","263","264","265","266","267","268","269","270","271","272","273","274","275","276","277","278","279","280","281","282","283","284","285","286","287","288","289","290","291","292","293","294","295","296","297","298","299","300","301","302","303","304","305","306","307","308","309","310","311","312","313","314","315","316","317","318","319","320","321","322","323","324","325","326","327","328","329","330","331","332","333","334","335","336","337","338","339","340","341","342","343","344","345","346","347","348","349","350","351","352","353","354","355","356","357","358","359","360","361","362","363","364","365","366","367","368","369","370","371","372","373","374","375","376","377","378","379","380","381","382","383","384","385","386","387","388","389","390","391","392","393","394","395","396","397","398","399","400","401","402","403","404","405","406","407","408","409","410","411","412","413","414","415","416","417","418","419","420","421","422","423","424","425","426","427","428","429","430","431","432","433","434","435","436","437","438","439","440","441","442","443","444","445","446","447","448","449","450","451","452","453","454","455","456","457","458","459","460","461","462","463","464","465","466","467","468","469","470","471","472","473","474","475","476","477","478","479","480","481","482","483","484","485","486","487","488","489","490","491","492","493","494","495","496","497","498","499","500","501","502","503","504","505","506","507","508","509","510","511","512","513","514","515","516","517","518","519","520","521","522","523","524","525","526","527","528","529","530","531","532","533","534","535","536","537","538","539","540","541","542","543","544","545","546","547","548","549","550","551","552","553","554","555","556","557","558","559","560","561","562","563","564","565","566","567","568","569","570","571","572","573","574","575","576","577","578","579","580","581","582","583","584","585","586","587","588","589","590","591","592","593","594","595","596","597","598","599","600","601","602","603","604","605","606","607","608","609","610","611","612","613","614","615","616","617","618","619","620","621","622","623","624","625","626","627","628","629","630","631","632","633","634","635","636","637","638","639","640","641","642","643","644","645","646","647","648","649","650","651","652","653","654","655","656","657","658","659","660","661","662","663","664","665","666","667","668","669","670","671","672","673","674","675","676","677","678","679","680","681","682","683","684","685","686","687","688","689","690","691","692","693","694","695","696","697","698","699","700","701","702","703","704","705","706","707","708","709","710","711","712","713","714","715","716","717","718","719","720","721","722","723","724","725","726","727","728","729","730","731","732","733","734","735","736","737","738","739","740","741","742","743","744","745","746","747","748","749","750","751","752","753","754","755","756","757","758","759","760","761","762","763","764","765","766","767","768","769","770","771","772","773","774","775","776","777","778","779","780","781","782","783","784","785","786","787","788","789","790","791","792","793","794","795","796","797","798","799","800","801","802","803","804","805","806","807","808","809","810","811","812","813","814","815","816","817","818","819","820","821","822","823","824","825","826","827","828","829","830","831","832","833","834","835","836","837","838","839","840","841","842","843","844","845","846","847","848","849","850","851","852","853","854","855","856","857","858","859","860","861","862","863","864","865","866","867","868","869","870","871","872","873","874","875","876","877","878","879","880","881","882","883","884","885","886","887","888","889","890","891","892","893","894","895","896","897","898","899","900","901","902","903","904","905","906","907","908","909","910","911","912","913","914","915","916","917","918","919","920","921","922","923","924","925","926","927","928","929","930","931","932","933","934","935","936","937","938","939","940","941","942","943","944","945","946","947","948","949","950","951","952","953","954","955","956","957","958","959","960","961","962","963","964","965","966","967","968","969","970","971","972","973","974","975","976","977","978","979","980","981","982","983","984","985","986","987","988","989","990","991","992","993","994","995","996","997","998","999","1000","1001","1002","1003","1004","1005","1006","1007","1008","1009","1010","1011","1012","1013","1014","1015","1016","1017","1018","1019","1020","1021","1022","1023","1024","1025","1026","1027","1028","1029","1030","1031","1032","1033","1034","1035","1036","1037","1038","1039","1040","1041","1042","1043","1044","1045","1046","1047","1048","1049","1050","1051","1052","1053","1054","1055","1056","1057","1058","1059","1060","1061","1062","1063","1064","1065","1066","1067","1068","1069","1070","1071","1072","1073","1074","1075","1076","1077","1078","1079","1080","1081","1082","1083","1084","1085","1086","1087","1088","1089","1090","1091","1092","1093","1094","1095","1096","1097","1098","1099","1100","1101","1102","1103","1104","1105","1106","1107","1108","1109","1110","1111","1112","1113","1114","1115","1116","1117","1118","1119","1120","1121","1122","1123","1124","1125","1126","1127","1128","1129","1130","1131","1132","1133","1134","1135","1136","1137","1138","1139","1140","1141","1142","1143","1144","1145","1146","1147","1148","1149","1150","1151","1152","1153","1154","1155","1156","1157","1158","1159","1160","1161","1162","1163","1164","1165","1166","1167","1168","1169","1170","1171","1172","1173","1174","1175","1176","1177","1178","1179","1180","1181","1182","1183","1184","1185","1186","1187","1188","1189","1190","1191","1192","1193","1194","1195","1196","1197","1198","1199","1200","1201","1202","1203","1204","1205","1206","1207","1208","1209","1210","1211","1212","1213","1214","1215","1216","1217","1218","1219","1220","1221","1222","1223","1224","1225","1226","1227","1228","1229","1230","1231","1232","1233","1234","1235","1236","1237","1238","1239","1240","1241","1242","1243","1244","1245","1246","1247","1248","1249","1250","1251","1252","1253","1254","1255","1256","1257","1258","1259","1260","1261","1262","1263","1264","1265","1266","1267","1268","1269","1270","1271","1272","1273","1274","1275","1276","1277","1278","1279","1280","1281","1282","1283","1284","1285","1286","1287","1288","1289","1290","1291","1292","1293","1294","1295","1296","1297","1298","1299","1300","1301","1302","1303","1304","1305","1306","1307","1308","1309","1310","1311","1312","1313","1314","1315","1316","1317","1318","1319","1320","1321","1322","1323","1324","1325","1326","1327","1328","1329","1330","1331","1332","1333","1334","1335","1336","1337","1338","1339","1340","1341","1342","1343","1344","1345","1346","1347","1348","1349","1350","1351","1352","1353","1354","1355","1356","1357","1358","1359","1360","1361","1362","1363","1364","1365","1366","1367","1368","1369","1370","1371","1372","1373","1374","1375","1376","1377","1378","1379","1380","1381","1382","1383","1384","1385","1386","1387","1388","1389","1390","1391","1392","1393","1394","1395","1396","1397","1398","1399","1400","1401","1402","1403","1404","1405","1406","1407","1408","1409","1410","1411","1412","1413","1414","1415","1416","1417","1418","1419","1420","1421","1422","1423","1424","1425","1426","1427","1428","1429","1430","1431","1432","1433","1434","1435","1436","1437","1438","1439","1440","1441","1442","1443","1444","1445","1446","1447","1448","1449","1450","1451","1452","1453","1454","1455","1456","1457","1458","1459","1460","1461","1462","1463","1464","1465","1466","1467","1468","1469","1470","1471","1472","1473","1474","1475","1476","1477","1478","1479","1480","1481","1482","1483","1484","1485","1486","1487","1488","1489","1490","1491","1492","1493","1494","1495","1496","1497","1498","1499","1500","1501","1502","1503","1504","1505","1506","1507","1508","1509","1510","1511","1512","1513","1514","1515","1516","1517","1518","1519","1520","1521","1522","1523","1524","1525","1526","1527","1528","1529","1530","1531","1532","1533","1534","1535","1536","1537","1538","1539","1540","1541","1542","1543","1544","1545","1546","1547","1548","1549","1550","1551","1552","1553","1554","1555","1556","1557","1558","1559","1560","1561","1562","1563","1564","1565","1566","1567","1568","1569","1570","1571","1572","1573","1574","1575","1576","1577","1578","1579","1580","1581","1582","1583","1584","1585","1586","1587","1588","1589","1590","1591","1592","1593","1594","1595","1596","1597","1598","1599","1600","1601","1602","1603","1604","1605","1606","1607","1608","1609","1610","1611","1612","1613","1614","1615","1616","1617","1618","1619","1620","1621","1622","1623","1624","1625","1626","1627","1628","1629","1630","1631","1632","1633","1634","1635","1636","1637","1638","1639","1640","1641","1642","1643","1644","1645","1646","1647","1648","1649","1650","1651","1652","1653","1654","1655","1656","1657","1658","1659","1660","1661","1662","1663","1664","1665","1666","1667","1668","1669","1670","1671","1672","1673","1674","1675","1676","1677","1678","1679","1680","1681","1682","1683","1684","1685","1686","1687","1688","1689","1690","1691","1692","1693","1694","1695","1696","1697","1698","1699","1700","1701","1702","1703","1704","1705","1706","1707","1708","1709","1710","1711","1712","1713","1714","1715","1716","1717","1718","1719","1720","1721","1722","1723","1724","1725","1726","1727","1728","1729","1730","1731","1732","1733","1734","1735","1736","1737","1738","1739","1740","1741","1742","1743","1744","1745","1746","1747","1748","1749","1750","1751","1752","1753","1754","1755","1756","1757","1758","1759","1760","1761","1762","1763","1764","1765","1766","1767","1768","1769","1770","1771","1772","1773","1774","1775","1776","1777","1778","1779","1780","1781","1782","1783","1784","1785","1786","1787","1788","1789","1790","1791","1792","1793","1794","1795","1796","1797","1798","1799","1800","1801","1802","1803","1804","1805","1806","1807","1808","1809","1810","1811","1812","1813","1814","1815","1816","1817","1818","1819","1820","1821","1822","1823","1824","1825","1826","1827","1828","1829","1830","1831","1832","1833","1834","1835","1836","1837","1838","1839","1840","1841","1842","1843","1844","1845","1846","1847","1848","1849","1850","1851","1852","1853","1854","1855","1856","1857","1858","1859","1860","1861","1862","1863","1864","1865","1866","1867","1868","1869","1870","1871","1872","1873","1874","1875","1876","1877","1878","1879","1880","1881","1882","1883","1884","1885","1886","1887","1888","1889","1890","1891","1892","1893","1894","1895","1896","1897","1898","1899","1900","1901","1902","1903","1904","1905","1906","1907","1908","1909","1910","1911","1912","1913","1914","1915","1916","1917","1918","1919","1920","1921","1922","1923","1924","1925","1926","1927","1928","1929","1930","1931","1932","1933","1934","1935","1936","1937","1938","1939","1940","1941","1942","1943","1944","1945","1946","1947","1948","1949","1950","1951","1952","1953","1954","1955","1956","1957","1958","1959","1960","1961","1962","1963","1964","1965","1966","1967","1968","1969","1970","1971","1972","1973","1974","1975","1976","1977","1978","1979","1980","1981","1982","1983","1984","1985","1986","1987","1988","1989","1990","1991","1992","1993","1994","1995","1996","1997","1998","1999","2000"],[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,12,13,14,15,16,17,18,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,1,2,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,1,2,3,4,5,6,7,8,9,10,11,12,13,14,16,17,18,19,20,21,22,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,1,2,3,4,5,6,7,8,9,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,1,2,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20],[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,26,26,26,26,26,26,26,26,26,26,26,26,26,26,26,26,26,26,26,26,26,27,27,27,27,27,27,27,27,27,27,27,27,27,27,27,27,27,27,27,27,28,28,28,28,28,28,28,28,28,28,28,28,28,28,28,28,28,28,28,28,29,29,29,29,29,29,29,29,29,29,29,29,29,29,29,29,29,30,30,30,30,30,30,30,30,30,30,30,30,30,30,30,30,30,31,31,31,31,31,31,31,31,31,31,31,31,31,31,31,31,31,31,31,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,32,33,33,33,33,33,33,33,33,33,33,33,33,33,33,33,33,33,33,33,34,34,34,34,34,34,34,34,34,34,34,34,34,34,34,34,34,34,34,34,34,34,35,35,35,35,35,35,35,35,35,35,35,35,35,35,35,35,35,35,35,35,36,36,36,36,36,36,36,36,36,36,36,36,36,36,36,36,36,36,36,37,37,37,37,37,37,37,37,37,37,37,37,37,37,37,37,37,37,37,38,38,38,38,38,38,38,38,38,38,38,38,38,38,38,38,38,39,39,39,39,39,39,39,39,39,39,39,39,39,39,39,39,40,40,40,40,40,40,40,40,40,40,40,40,40,40,40,40,40,40,40,40,41,41,41,41,41,41,41,41,41,41,41,41,41,41,41,41,41,41,41,42,42,42,42,42,42,42,42,42,42,42,42,42,42,42,42,42,42,42,42,42,43,43,43,43,43,43,43,43,43,43,43,43,43,43,43,43,43,44,44,44,44,44,44,44,44,44,44,44,44,44,44,44,44,44,44,44,45,45,45,45,45,45,45,45,45,45,45,45,45,45,45,45,45,45,45,46,46,46,46,46,46,46,46,46,46,46,46,46,46,46,46,46,46,46,46,46,46,46,47,47,47,47,47,47,47,47,47,47,47,47,47,47,47,47,47,48,48,48,48,48,48,48,48,48,48,48,48,48,48,48,48,48,48,48,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,51,51,51,51,51,51,51,51,51,51,51,51,51,51,51,51,51,51,51,51,51,51,51,52,52,52,52,52,52,52,52,52,52,52,52,52,52,52,52,52,52,52,52,52,52,52,53,53,53,53,53,53,53,53,53,53,53,53,53,53,53,53,53,53,53,54,54,54,54,54,54,54,54,54,54,54,54,54,54,54,54,54,54,54,55,55,55,55,55,55,55,55,55,55,55,55,55,55,55,55,55,55,55,55,55,56,56,56,56,56,56,56,56,56,56,56,56,56,56,56,56,56,56,56,57,57,57,57,57,57,57,57,57,57,57,57,57,57,57,57,57,57,58,58,58,58,58,58,58,58,58,58,58,58,58,58,58,58,58,58,58,58,59,59,59,59,59,59,59,59,59,59,59,59,59,59,59,59,59,60,60,60,60,60,60,60,60,60,60,60,60,60,60,60,60,60,60,60,60,60,61,61,61,61,61,61,61,61,61,61,61,61,61,61,61,61,61,61,61,62,62,62,62,62,62,62,62,62,62,62,62,62,62,62,62,62,62,62,62,63,63,63,63,63,63,63,63,63,63,63,63,63,63,63,63,63,63,63,63,63,63,63,63,63,64,64,64,64,64,64,64,64,64,64,64,64,64,64,64,64,64,64,64,65,65,65,65,65,65,65,65,65,65,65,65,65,65,65,65,65,65,65,65,65,65,66,66,66,66,66,66,66,66,66,66,66,66,66,66,66,66,66,66,66,66,67,67,67,67,67,67,67,67,67,67,67,67,67,67,67,67,67,67,67,67,67,68,68,68,68,68,68,68,68,68,68,68,68,68,68,68,68,68,69,69,69,69,69,69,69,69,69,69,69,69,69,69,69,69,69,69,70,70,70,70,70,70,70,70,70,70,70,70,70,70,70,70,70,70,70,70,70,71,71,71,71,71,71,71,71,71,71,71,71,71,71,71,71,71,71,71,71,71,71,72,72,72,72,72,72,72,72,72,72,72,72,72,72,72,72,72,72,72,72,72,73,73,73,73,73,73,73,73,73,73,73,73,73,73,73,73,73,73,73,73,74,74,74,74,74,74,74,74,74,74,74,74,74,74,74,74,74,75,75,75,75,75,75,75,75,75,75,75,75,75,75,75,75,75,76,76,76,76,76,76,76,76,76,76,76,76,76,76,76,76,76,76,77,77,77,77,77,77,77,77,77,77,77,77,77,77,77,77,77,77,77,78,78,78,78,78,78,78,78,78,78,78,78,78,78,78,78,78,78,79,79,79,79,79,79,79,79,79,79,79,79,79,79,79,79,79,79,79,79,80,80,80,80,80,80,80,80,80,80,80,80,80,80,80,80,80,80,80,80,81,81,81,81,81,81,81,81,81,81,81,81,81,81,81,81,81,81,81,81,81,82,82,82,82,82,82,82,82,82,82,82,82,82,82,82,82,82,82,82,82,82,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,84,84,84,84,84,84,84,84,84,84,84,84,84,84,84,84,84,84,84,84,84,85,85,85,85,85,85,85,85,85,85,85,85,85,85,85,85,85,85,85,85,85,85,86,86,86,86,86,86,86,86,86,86,86,86,86,86,86,86,86,86,86,86,86,86,87,87,87,87,87,87,87,87,87,87,87,87,87,87,87,87,87,87,87,87,87,88,88,88,88,88,88,88,88,88,88,88,88,88,88,88,88,88,88,88,88,88,88,88,89,89,89,89,89,89,89,89,89,89,89,89,89,89,89,89,89,89,90,90,90,90,90,90,90,90,90,90,90,90,90,90,90,90,90,90,90,90,90,90,90,91,91,91,91,91,91,91,91,91,91,91,91,91,91,91,91,91,91,92,92,92,92,92,92,92,92,92,92,92,92,92,92,92,92,92,93,93,93,93,93,93,93,93,93,93,93,93,93,93,93,93,93,93,93,93,94,94,94,94,94,94,94,94,94,94,94,94,94,94,94,94,95,95,95,95,95,95,95,95,95,95,95,95,95,95,95,95,95,95,95,95,95,96,96,96,96,96,96,96,96,96,96,96,96,96,96,96,96,96,96,96,96,96,97,97,97,97,97,97,97,97,97,97,97,97,97,97,97,97,97,97,97,97,97,98,98,98,98,98,98,98,98,98,98,98,98,98,98,98,98,98,98,98,98,98,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100],[5,7,4,3,5,4,5,4,5,5,5,5,5,5,5,6,4,4,7,4,8,4,6,5,5,5,4,5,6,4,6,4,4,3,6,5,5,3,4,5,5,5,4,4,6,5,5,7,4,7,6,4,5,4,6,7,6,4,3,2,5,6,6,3,6,4,5,6,6,4,3,5,6,5,4,5,4,6,4,5,7,7,4,5,4,6,7,6,4,6,8,7,6,7,6,6,5,6,6,6,5,6,4,6,5,5,4,4,6,5,4,7,5,6,5,3,4,6,5,7,5,4,6,4,4,4,4,5,4,5,6,5,5,6,4,4,7,5,6,5,5,7,5,6,5,4,7,6,7,6,5,6,5,4,5,5,5,7,5,5,7,6,5,6,5,5,6,6,5,5,5,5,5,3,4,4,5,4,6,6,7,6,4,5,6,5,4,5,6,5,5,6,5,6,6,7,6,3,5,3,6,3,6,4,6,4,5,4,5,5,6,5,6,5,7,4,5,6,6,6,6,4,5,5,6,4,5,5,4,5,4,2,7,4,3,4,6,5,3,4,3,4,4,4,5,6,4,4,6,6,5,4,6,6,6,7,3,4,4,6,6,4,7,5,5,4,7,6,9,7,6,8,5,6,6,8,7,7,7,7,6,8,6,5,5,4,4,7,6,6,8,5,8,5,7,6,5,6,5,6,6,6,4,3,5,5,4,5,6,5,7,5,5,6,8,5,6,8,6,7,5,4,6,6,4,3,6,5,3,5,6,4,5,5,6,4,6,6,6,6,3,5,4,7,5,4,4,4,5,4,7,5,4,5,5,4,5,3,5,4,5,6,5,4,5,5,6,5,4,3,5,8,4,5,5,5,3,5,4,5,4,6,4,6,5,3,5,4,5,3,4,5,7,5,4,5,6,8,5,5,4,4,6,7,4,6,5,6,5,6,5,5,5,5,4,7,5,5,4,6,3,6,6,4,4,5,4,5,4,3,6,4,5,6,3,2,6,6,5,4,4,6,4,5,5,6,6,7,5,5,4,6,5,7,6,6,4,5,5,7,5,4,6,5,5,6,4,6,5,6,5,5,7,3,7,3,5,4,5,5,7,7,7,6,5,6,7,6,6,5,5,7,5,5,6,4,5,5,4,7,6,5,6,4,5,6,6,5,4,5,4,5,5,5,5,5,4,6,4,4,4,6,5,4,4,6,5,4,6,4,3,7,4,7,5,4,4,6,6,5,4,7,5,7,5,5,5,6,5,5,4,5,5,4,6,6,5,3,3,5,6,6,6,5,6,5,6,5,6,7,5,6,5,4,3,4,4,4,5,7,4,4,6,5,4,5,3,3,5,5,5,3,2,6,5,5,7,5,6,6,8,5,5,6,5,4,5,8,6,8,6,6,6,6,5,5,6,5,5,6,5,3,4,4,4,6,3,6,5,5,6,6,6,6,4,4,5,3,4,6,6,5,4,5,5,5,5,6,6,4,5,6,7,7,7,8,6,7,8,7,8,8,9,6,7,6,7,7,7,9,6,6,5,8,7,6,5,6,7,4,6,6,4,5,5,3,6,5,7,6,5,6,5,4,5,6,4,4,5,6,4,4,7,4,6,3,6,4,5,6,4,5,3,6,4,5,4,6,3,3,4,6,4,3,5,3,4,7,6,5,4,4,5,5,6,6,5,6,7,5,6,6,4,4,4,5,5,4,6,7,6,5,5,5,5,5,5,4,6,4,4,4,6,4,5,5,6,5,4,4,4,6,4,4,7,5,5,5,6,5,4,3,4,6,8,8,9,9,8,10,9,10,9,8,7,10,8,9,10,9,8,6,8,8,6,3,5,5,6,5,5,5,5,4,6,5,5,6,5,4,3,5,4,3,7,5,5,5,4,3,5,5,7,7,5,6,3,6,6,6,5,5,4,4,7,5,5,4,6,4,6,5,5,5,5,4,6,5,7,4,6,5,6,6,6,5,5,4,5,6,4,6,8,5,7,7,5,6,5,5,6,6,5,7,6,4,5,3,6,6,5,5,4,6,4,5,6,5,5,4,4,6,4,4,4,6,4,4,6,5,6,6,5,4,5,8,3,2,6,3,4,4,4,8,5,5,6,4,5,6,6,4,5,5,5,5,4,4,7,6,4,7,5,6,6,4,8,4,5,5,5,6,8,7,6,6,5,5,4,6,4,7,5,5,5,6,5,5,5,6,6,5,6,5,6,8,4,5,4,6,5,5,6,2,5,5,7,5,6,5,4,5,5,5,5,6,5,4,5,4,5,6,5,4,5,5,5,5,5,6,3,5,5,6,5,5,5,3,5,6,5,6,3,6,5,4,4,6,6,5,5,6,5,2,5,5,5,7,5,5,6,6,6,6,3,5,4,5,4,5,7,5,6,4,1,4,4,5,5,6,6,5,4,4,6,5,5,6,4,5,5,7,4,5,6,5,5,6,6,4,6,4,5,6,6,5,5,3,6,6,5,7,7,6,5,5,6,6,4,7,6,5,4,5,4,6,4,6,5,5,3,6,4,6,5,5,5,4,4,6,5,5,6,8,6,7,7,6,5,5,5,6,5,7,4,7,2,7,8,5,4,6,5,6,6,3,6,3,4,5,6,2,6,4,5,5,4,5,5,3,6,5,6,5,5,6,5,6,5,7,6,4,4,6,6,5,6,5,8,9,7,6,7,8,5,6,7,8,7,6,7,7,7,7,4,5,6,4,3,6,4,3,4,5,4,6,4,4,5,3,6,5,4,5,4,4,5,5,5,5,6,3,4,5,4,4,6,4,6,4,6,5,5,4,5,5,5,6,5,3,4,6,5,7,5,5,5,6,5,7,5,6,5,4,4,4,4,7,4,5,4,4,2,4,4,5,3,3,5,5,6,6,5,2,7,5,5,5,3,6,6,5,3,4,5,4,5,5,4,7,5,5,6,4,4,5,5,4,5,3,5,4,6,7,7,5,5,5,5,6,6,5,6,6,5,4,5,7,6,4,4,7,5,6,8,6,3,7,5,5,4,4,7,5,6,4,5,4,4,1,7,5,5,6,3,6,5,5,4,6,6,6,5,4,4,6,5,3,4,4,4,5,5,4,3,6,5,3,5,4,5,3,3,4,5,5,5,5,6,4,4,6,4,5,4,5,6,3,4,6,7,5,5,5,4,4,5,7,1,3,3,5,3,4,7,4,7,6,4,5,4,6,5,4,5,4,3,3,3,4,5,3,5,4,6,5,5,5,6,7,5,5,6,4,4,4,6,4,5,5,4,6,5,3,6,5,5,6,5,6,5,5,4,6,4,5,4,6,3,5,5,6,4,6,5,5,5,6,5,5,7,5,6,5,6,5,5,3,5,4,4,6,4,5,6,4,3,6,4,5,3,5,6,6,5,5,5,6,5,5,5,6,5,6,3,5,5,5,5,5,4,5,5,4,4,8,7,6,7,7,5,6,5,7,6,5,6,7,7,5,6,6,7,7,5,6,4,7,5,5,6,6,5,3,4,6,3,7,6,4,3,7,6,6,6,4,7,4,5,5,3,5,6,6,5,5,6,4,5,6,5,6,4,4,4,5,5,6,4,4,6,5,6,5,5,5,6,5,2,4,6,4,4,6,6,6,6,5,5,5,6,4,7,5,6,7,5,4,6,5,6,5,7,4,5,6,9,5,5,7,6,5,5,5,5,4,6,6,5,6,6,6,5,7,4,6,5,6,7,5,7,3,5,5,4,6,5,4,4,6,7,5,5,4,5,5,6,6,3,5,5,5,6,5,4,5,5,5,4,5,4,4,3,7,3,6,5,6,6,4,5,4,5,7,5,5,6,4,5,5,5,4,4,7,4,4,6,7,7,6,6,7,7,7,6,6,5,7,5,6,7,8,4,6,4,4,7,7,7,8,10,8,8,6,9,8,8,5,6,9,8,8,7,10,9,8,9,8,6,4,6,5,5,4,5,4,6,5,6,4,4,7,4,3,5,5,5,7,4,4,4,4,7,5,5,6,5,5,5,4,5,7,6,6,4,5,5,5,6,7,6,7,7,5,7,9,6,7,7,7,8,8,8,7,9,8,7,8,6,7,6,8,7,4,3,5,5,4,7,4,5,5,6,5,4,7,4,5,7,7,4,4,4,4,4,6,4,5,4,3,5,6,3,4,4,5,4,5,7,4,5,6,5,7,5,5,5,6,6,5,7,6,3,5,5,4,5,5,5,4,5,6,6,6,6,5,5,2,5,7,3,4,4,5,5,3,7,5,3,5,4,5,5,6,6,6,4,5,5,5,6,7,5,4,6,5,6,6,5,6,6,6,4,4,5,4,8,5,5,6,4,3,5,4,5,5,7,5,3,4,5,5,4,5,5,4,4,4,4,3,6,4,7,6,5,5,3,4,4,6,5,7,5,5,5,3,5,6,6,5,6,5,4,4,7,5,6,5,5,3,5,5,4,6,6,5,5,4,6,4,5,4,5,3,4,5,5,5,5,5,5,6,7,3,7,7,7,5,5,5,5,6,7,5,5,4,4,8,5,9],["girl","boy","girl","girl","girl","boy","boy","boy","boy","boy","girl","girl","boy","girl","girl","girl","boy","boy","girl","boy","girl","boy","boy","girl","girl","boy","girl","boy","girl","girl","girl","boy","boy","boy","boy","girl","girl","girl","boy","boy","boy","girl","girl","girl","boy","girl","boy","girl","girl","girl","girl","girl","girl","girl","boy","boy","girl","boy","girl","girl","girl","girl","girl","boy","boy","boy","boy","girl","boy","boy","boy","boy","boy","girl","girl","boy","boy","boy","boy","girl","boy","boy","girl","boy","girl","boy","boy","boy","girl","girl","boy","girl","girl","boy","girl","boy","girl","girl","boy","girl","boy","boy","boy","girl","girl","girl","girl","girl","boy","boy","girl","girl","boy","girl","girl","boy","girl","boy","boy","boy","boy","boy","girl","girl","boy","boy","boy","girl","boy","girl","boy","girl","boy","boy","boy","girl","boy","boy","girl","boy","girl","girl","boy","girl","boy","girl","girl","boy","girl","boy","girl","boy","girl","boy","boy","boy","girl","boy","boy","girl","girl","girl","girl","boy","girl","girl","girl","girl","boy","boy","boy","boy","boy","boy","girl","boy","boy","boy","boy","girl","girl","girl","boy","boy","girl","boy","girl","boy","girl","boy","boy","girl","girl","boy","boy","girl","boy","boy","boy","boy","boy","girl","girl","girl","girl","girl","girl","boy","girl","girl","boy","boy","girl","boy","girl","girl","girl","boy","boy","boy","girl","girl","boy","boy","boy","boy","girl","girl","boy","boy","girl","girl","girl","girl","boy","boy","boy","girl","girl","boy","boy","girl","boy","boy","boy","boy","girl","girl","boy","boy","girl","girl","boy","girl","boy","boy","girl","girl","boy","girl","boy","boy","girl","girl","girl","girl","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","girl","girl","girl","boy","boy","girl","boy","boy","girl","boy","girl","boy","girl","boy","girl","boy","boy","boy","boy","girl","girl","girl","girl","girl","boy","girl","boy","girl","girl","girl","girl","girl","boy","girl","girl","girl","boy","girl","boy","boy","girl","boy","girl","girl","girl","girl","girl","boy","boy","girl","boy","girl","girl","girl","boy","girl","girl","boy","boy","boy","boy","boy","boy","girl","boy","boy","boy","girl","boy","girl","boy","girl","boy","girl","boy","boy","girl","boy","boy","girl","girl","girl","boy","girl","boy","boy","girl","boy","boy","boy","girl","boy","girl","girl","boy","girl","girl","boy","girl","girl","boy","girl","boy","girl","girl","girl","girl","girl","girl","girl","boy","girl","boy","boy","girl","boy","girl","girl","boy","girl","girl","girl","boy","girl","girl","girl","girl","boy","boy","boy","girl","boy","boy","girl","boy","boy","boy","girl","boy","boy","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","boy","boy","boy","girl","girl","boy","boy","boy","girl","girl","boy","girl","boy","girl","girl","girl","boy","girl","girl","boy","girl","girl","girl","boy","boy","boy","boy","girl","boy","girl","girl","boy","girl","boy","girl","boy","boy","boy","boy","boy","girl","girl","girl","girl","boy","girl","boy","girl","boy","boy","boy","boy","boy","girl","girl","girl","boy","boy","girl","girl","girl","girl","boy","boy","girl","girl","boy","girl","boy","girl","girl","girl","boy","boy","boy","boy","boy","girl","girl","boy","girl","boy","girl","girl","boy","boy","boy","girl","boy","girl","boy","boy","girl","girl","girl","boy","boy","girl","boy","boy","boy","boy","boy","boy","boy","boy","girl","boy","girl","girl","boy","girl","girl","girl","boy","boy","boy","boy","boy","girl","boy","boy","girl","girl","boy","girl","girl","girl","boy","boy","girl","boy","girl","boy","girl","boy","girl","girl","girl","boy","boy","boy","girl","girl","boy","girl","girl","girl","boy","boy","girl","girl","girl","girl","boy","boy","boy","girl","boy","girl","boy","boy","girl","boy","girl","boy","girl","girl","boy","girl","girl","girl","boy","girl","girl","girl","boy","girl","girl","girl","boy","boy","boy","boy","boy","boy","boy","girl","boy","boy","girl","girl","boy","girl","girl","boy","boy","boy","girl","boy","girl","girl","boy","girl","boy","girl","boy","boy","boy","boy","girl","boy","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","boy","boy","girl","boy","boy","boy","boy","boy","girl","boy","boy","girl","boy","boy","girl","boy","boy","girl","boy","boy","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","boy","boy","boy","boy","girl","girl","girl","boy","girl","boy","boy","girl","girl","boy","girl","boy","boy","boy","boy","girl","girl","girl","boy","boy","boy","girl","boy","boy","girl","boy","boy","boy","boy","boy","boy","girl","girl","boy","boy","boy","girl","girl","girl","girl","boy","girl","boy","boy","boy","boy","boy","girl","girl","boy","girl","girl","boy","boy","girl","girl","girl","girl","girl","girl","boy","boy","boy","girl","boy","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","boy","boy","girl","boy","boy","boy","girl","girl","girl","girl","boy","boy","boy","girl","girl","girl","girl","boy","girl","boy","boy","girl","boy","girl","boy","girl","girl","girl","boy","girl","girl","girl","boy","boy","girl","boy","girl","girl","girl","boy","girl","boy","girl","girl","girl","boy","boy","girl","boy","boy","boy","boy","boy","boy","boy","boy","boy","girl","girl","girl","boy","boy","girl","boy","boy","boy","boy","girl","girl","girl","girl","boy","boy","girl","boy","boy","girl","girl","girl","boy","boy","boy","girl","boy","girl","boy","boy","boy","boy","boy","boy","girl","boy","boy","girl","girl","girl","boy","boy","boy","girl","girl","boy","girl","girl","girl","girl","girl","boy","boy","girl","boy","girl","girl","girl","girl","boy","girl","boy","girl","boy","boy","girl","boy","girl","girl","girl","boy","girl","boy","boy","girl","girl","boy","girl","boy","boy","boy","boy","boy","girl","girl","boy","girl","boy","boy","girl","girl","boy","girl","girl","boy","boy","girl","girl","boy","girl","girl","boy","girl","boy","boy","girl","girl","girl","girl","boy","girl","boy","boy","girl","boy","boy","boy","girl","girl","boy","boy","girl","boy","boy","boy","boy","girl","boy","girl","boy","boy","girl","boy","girl","girl","girl","boy","girl","boy","girl","girl","girl","girl","boy","girl","girl","boy","boy","boy","girl","girl","boy","girl","girl","boy","boy","girl","girl","boy","girl","boy","girl","girl","girl","boy","boy","boy","girl","girl","girl","boy","boy","boy","boy","boy","girl","boy","girl","boy","girl","girl","boy","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","boy","boy","boy","boy","boy","girl","boy","boy","boy","girl","boy","boy","girl","girl","girl","boy","girl","girl","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","girl","boy","boy","girl","girl","boy","boy","girl","girl","girl","girl","boy","boy","girl","boy","boy","girl","girl","girl","boy","boy","girl","girl","boy","girl","girl","boy","girl","girl","boy","girl","boy","girl","boy","girl","boy","girl","girl","girl","boy","boy","girl","boy","girl","boy","girl","boy","girl","boy","girl","girl","girl","girl","boy","boy","boy","girl","girl","boy","boy","boy","boy","girl","girl","boy","boy","boy","girl","girl","girl","boy","boy","boy","girl","boy","girl","girl","boy","girl","girl","boy","boy","girl","boy","girl","girl","girl","girl","boy","boy","boy","girl","boy","girl","boy","girl","girl","girl","boy","girl","girl","boy","girl","girl","boy","girl","girl","boy","boy","girl","boy","boy","girl","boy","boy","boy","boy","girl","girl","girl","girl","girl","girl","girl","boy","boy","boy","girl","boy","boy","girl","boy","girl","boy","girl","boy","boy","boy","boy","girl","boy","girl","boy","girl","boy","boy","girl","girl","boy","girl","boy","girl","girl","girl","girl","boy","boy","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","boy","boy","boy","girl","girl","girl","boy","boy","boy","girl","girl","boy","boy","girl","boy","girl","boy","boy","boy","girl","girl","girl","girl","girl","boy","boy","girl","girl","girl","girl","girl","girl","boy","girl","girl","girl","girl","boy","boy","boy","girl","boy","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","boy","boy","boy","boy","boy","girl","boy","boy","girl","girl","boy","boy","girl","girl","boy","boy","boy","boy","girl","boy","girl","boy","boy","boy","girl","boy","girl","boy","boy","boy","girl","boy","girl","girl","girl","girl","girl","girl","girl","girl","girl","boy","boy","boy","girl","boy","boy","boy","boy","girl","boy","girl","girl","boy","boy","boy","boy","boy","boy","girl","boy","boy","girl","girl","boy","girl","boy","girl","girl","boy","girl","girl","boy","boy","girl","girl","girl","girl","boy","boy","boy","boy","boy","boy","girl","girl","boy","boy","boy","boy","girl","boy","boy","boy","boy","boy","girl","boy","boy","girl","girl","girl","girl","boy","boy","boy","girl","girl","boy","girl","girl","boy","boy","boy","boy","boy","girl","girl","boy","girl","boy","girl","boy","boy","girl","boy","boy","boy","boy","boy","girl","girl","boy","girl","girl","boy","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","boy","girl","boy","girl","girl","boy","boy","girl","girl","boy","boy","girl","boy","boy","boy","girl","girl","boy","boy","girl","girl","girl","girl","boy","girl","boy","girl","boy","boy","boy","boy","boy","boy","boy","girl","girl","boy","boy","girl","girl","boy","boy","girl","boy","girl","boy","boy","boy","boy","girl","girl","boy","boy","girl","girl","girl","boy","boy","boy","girl","boy","boy","boy","boy","girl","girl","girl","girl","boy","girl","boy","boy","boy","boy","boy","boy","girl","boy","girl","boy","boy","boy","girl","girl","boy","boy","boy","girl","girl","boy","boy","boy","girl","girl","girl","boy","boy","boy","girl","girl","girl","boy","girl","girl","boy","boy","girl","boy","girl","boy","boy","boy","girl","girl","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","girl","girl","girl","boy","girl","girl","girl","boy","girl","girl","girl","girl","boy","girl","boy","boy","girl","boy","girl","girl","boy","boy","girl","boy","boy","girl","girl","boy","boy","boy","girl","girl","boy","girl","girl","girl","boy","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","girl","boy","girl","boy","boy","girl","girl","girl","boy","boy","boy","boy","boy","girl","boy","girl","girl","girl","girl","boy","boy","boy","girl","boy","girl","girl","girl","girl","boy","girl","girl","boy","girl","boy","boy","girl","girl","girl","boy","boy","girl","boy","boy","girl","girl","boy","girl","girl","girl","girl","girl","boy","boy","boy","girl","girl","boy","boy","boy","girl","girl","boy","boy","girl","boy","boy","boy","girl","girl","girl","boy","girl","girl","girl","girl","boy","boy","girl","girl","boy","boy","boy","boy","girl","boy","girl","boy","boy","boy","girl","boy","girl","boy","girl","girl","boy","girl","girl","girl","girl","girl","girl","girl","boy","girl","girl","boy","boy","boy","girl","girl","boy","girl","boy","girl","boy","boy","boy","girl","girl","boy","girl","girl","boy","boy","girl","boy","boy","boy","boy","girl","girl","boy","boy","boy","boy","girl","boy","boy","girl","boy","boy","boy","girl","girl","girl","boy","boy","girl","boy","boy","boy","girl","boy","boy","boy","girl","girl","boy","girl","boy","boy","boy","boy","boy","girl","girl","boy","girl","girl","girl","girl","boy","boy","boy","girl","boy","boy","girl","boy","girl","boy","boy","boy","girl","boy","boy","girl","boy","boy","girl","girl","girl","girl","girl","girl","boy","boy","girl","boy","girl","girl","boy","boy","boy","girl","boy","boy","boy","girl","girl","girl","boy","boy","girl","girl","girl","boy","boy","boy","girl","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","boy","girl","boy","girl","girl","girl","boy","girl","boy","boy","girl","girl","boy","girl","girl","boy","girl","girl","girl","girl","girl","boy","boy","boy","boy","girl","girl","boy","girl","girl","girl","boy","girl","boy","boy","girl","boy","boy","boy","girl","girl","boy","boy","boy","boy","boy","girl","boy","girl","girl","boy","boy","boy","boy","boy","girl","girl","girl","girl","girl","boy","girl","boy","boy"],[24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,12,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,18,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,19,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,14,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,17,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,23,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,24,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,22,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,16,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,15,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,13,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,25,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,21,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7],[6.3,4.9,5.3,4.7,6,4.7,5.9,4.2,5.2,3.9,5.7,4.8,5,5.5,6,5.7,3.2,3.1,6.6,4.8,6.4,2.4,3.7,4.4,4.3,4,3.8,4.2,5.1,4.1,4.6,4.9,3.1,3.2,4.4,3.7,6.1,3.5,2.9,3.3,4.2,6,4.6,4.9,4.7,4.8,2.8,6.7,4.9,6.3,5.6,3.1,3.5,4.7,4.3,4.9,5.9,2.6,4.1,5.3,6.1,6,6.3,4,5.3,5.6,5.2,6.2,6.1,3.9,4.8,5.8,4.9,6.6,5.6,4.5,5.4,4.9,5.4,6.7,6.3,4.2,4,4.7,4.7,5.2,5.8,4.4,3.8,5.9,7,7.3,5.6,5.6,6.3,4.2,4.6,6.1,5,5.8,5.5,5.3,4.1,5.8,4.2,3.9,5,4.4,4.3,3.3,3.1,6.4,3.5,5.9,4.2,3.5,4.6,5.1,4.2,4.9,3.6,2.7,5.8,4.8,4.4,1.7,3.6,3.8,4.1,5.7,2.9,4.9,5.1,4,3,4.7,2.8,3.7,5.1,3.5,4.7,6,4,6.1,3.2,3.3,5,4.2,5.6,3.9,4.5,2.2,4.2,1.5,3.2,2.7,4.1,4.8,3.5,3.6,5.5,4.8,3.5,5.2,6,5.1,5.3,6.7,3.6,3.5,3.9,4.3,4,4.6,4.5,3.6,2.6,3.9,5,4.5,7.3,6.7,2.9,5.4,6.3,3.4,4.9,5.1,7,5.4,4.9,6.6,5.8,4.4,4.9,6,4.8,3.6,5,5.5,5,5.2,5.4,6,5.7,6.1,5.2,4.7,5.5,4.8,4.9,4.6,4.6,3.4,5.6,5.4,5.6,3.2,5.1,4.4,4.8,4.2,4.3,4.2,4,1.6,4.9,3.8,4.1,3.7,4.8,4.2,5.7,4.6,3.8,2.8,4.7,5.6,2.8,3.8,2.4,5.3,3.5,4.5,4.5,4.5,6.5,6.4,6.2,6.1,5.6,6.3,6.2,6.2,5.7,5.9,5,6.1,4.5,7.2,6.3,4.8,8,6,7.7,6.1,3,3.3,5.3,3.2,3.6,4.5,1.4,2.3,2.8,4.5,3.9,4.5,3.1,4.5,2.3,6.5,3.1,4.2,3.4,4,3.1,6.3,4.4,5.5,7.9,2.9,6.4,5.1,4.3,4.3,5.8,4.5,4.5,6,5.6,4.7,4.5,4.3,3.2,5,2.9,4.2,5.6,4.5,6.3,5.1,2.8,6.3,3.1,5.4,4.7,6.5,4.5,6.8,2.9,5.1,4.2,5.1,3.7,5.2,6.3,3.9,5.3,3.7,5.8,4.6,5.9,5.8,6.6,3.7,5.8,6.2,4.8,7,5.4,7,3.3,6.7,5.6,3.5,3.6,5.1,3.7,5.3,6.1,7.8,4.8,6.7,5.1,6.8,7.1,6.7,5.6,5.1,4.8,6.7,6.7,6.9,7.9,6.6,6.9,5.7,4.4,5.7,6,7.1,5.4,6.2,7.1,4.4,3.2,5.6,6.2,4.5,5.9,5.9,3.7,7.1,5.6,5,5.9,4.8,5.7,6.8,4,6,6.5,5.9,5.1,5.8,6.9,7.2,3.3,6.6,2.7,3.1,5.7,5.6,6.3,5.9,2.9,6.3,5.7,6.3,4.2,5.4,5.7,4.2,3.5,4.6,4.1,4.2,4.6,4,4.5,4.9,5.3,3.7,3.8,5.8,3.7,5.4,6.7,4.7,6,6.3,5,5.1,5.7,5.8,7.6,7.8,5.4,5.7,6.3,6.7,7,5.6,5.5,5.4,6.7,7.3,6.1,6.5,5.8,7.1,5.9,7,5,4.8,5.9,4.5,6.3,6,6.4,3.3,4.6,5.6,4.5,6.4,3.8,6.6,6.5,5.6,5.7,4.2,6.7,3.2,5.4,4.7,3.4,2.7,3.8,3.7,7.3,6.6,3,5.2,4.7,6.2,4.5,3.3,3.9,3.4,4.1,5.3,5.6,5.3,4.5,5.1,5.6,5.6,5.9,6.5,3.7,3.9,5.7,5.7,5.1,5.7,4.6,7,4.7,3.3,4,2.9,3.8,3.7,4.3,4.1,3.7,4.1,4.1,2.8,3.2,6,3.2,3.4,3.2,4.9,3.5,3.9,3.8,2.9,3.6,6.1,5.5,6.2,2.6,4.5,2.5,6,3.6,4.8,2.9,6.2,4,4.9,5.4,4.2,4.8,6.4,3.2,5.2,3.4,4.8,4.2,3.2,4.7,4.6,4.9,4.3,3.8,4.1,5.5,5,3.6,5.4,6,4.8,4.1,4.2,5.6,4.4,4.8,3.3,4.9,3.4,3.7,4.4,5.9,3.8,5.2,6.1,5.5,7.2,6.2,7.1,6,6,5.2,6.6,5.7,6.9,6.6,5.7,4.7,3.3,2.6,5.3,4,4.7,5.2,3.5,6.5,3.9,4.9,3.6,4.3,3.5,4,7.1,6.1,4.6,4.9,5.7,5.2,7.3,3.5,4,5.8,5.8,4.4,4.6,4.2,1.5,2.9,3.2,1.8,5.5,0.4,5.4,5.1,6.2,5.9,4.9,6,4.9,3.9,4.5,4.6,2.4,4.7,5,5.8,6.1,4.6,5.2,4.8,4,3.1,4.8,7.3,3.3,4.2,6.9,7.2,8.7,5.4,9.2,7,6.4,9.5,8.1,6,7,8.1,7.4,8.4,4.7,7.4,5.7,8,8.8,6.2,5.8,3.8,8.5,4.6,3.9,3.9,4.7,5.6,3.3,5.7,4.1,4.3,5.4,4.8,3.2,4.2,3.9,6.1,4.5,3.8,6.8,5,6,7.5,7.9,7.8,7.9,7,5.5,7,6.2,7,6.6,6.8,6.8,6.8,7.4,7.5,7.1,6.7,7.3,6.7,6.3,3.9,4,3.2,4.2,5,5.3,5.3,5.7,5.2,5,3.9,5.4,7.4,4.3,6.7,4.4,5.3,5.3,4.6,6.9,6.4,6.7,4.1,4.6,5.3,7.1,6,4,4.9,4.1,4.4,4.8,4.5,3.6,5.7,6.8,7.3,3.5,3.5,4.9,4.8,5.8,5.9,5,4.3,4.6,3.6,3,4.5,3.9,4.2,6,6.5,3.4,5.4,5.6,3.6,4.7,5.7,4.8,6.4,4.9,5.3,5.5,3.9,5.1,4.8,4.6,5.2,6,6.4,5.1,7.7,7.4,6.8,6.8,8.2,7.6,7.5,6.5,4.3,7.7,7.5,6.5,8.6,5.4,4.5,3.8,6.9,6.6,5,3.4,2.5,5,3.8,3.4,3,4.4,3.6,4.2,5.3,2.9,2.8,3.7,4.2,3.2,3.6,4.1,3.2,5.3,6.6,4.1,5.5,4.8,4.5,3.9,5.9,5,7.1,5.2,7,7.3,4.1,5.5,4.9,7.2,4.1,4.4,5.3,3.6,6.7,4.2,5.6,4.7,5.6,6.2,4.7,5.4,6.7,4.8,5.5,5.6,4.3,5.2,5.9,4.5,5.7,4.2,6.7,6,6,4,5.1,4.9,3.9,4.5,3.3,4.3,6.4,5.2,6.2,5.7,3.6,5.1,5.1,3.7,4.3,7.9,4.8,7.7,6.3,4.9,5.2,7.9,6.2,6,4.8,6.2,5.6,5.1,4.5,5.5,7.1,4.8,4.9,5.5,5.5,6.1,4,3.5,3.4,6.2,5.1,3.5,6.3,6.1,5.7,3.9,5.6,3.6,5.2,8.4,3.1,5.1,6.5,4.5,5.3,3.7,5.3,5.5,5.8,3.7,5.4,4.9,4.1,5.5,6.1,3.9,5.2,4.4,4.3,3,5.9,4.4,5.5,5.8,1.8,5.5,2.1,3.6,1.9,4.4,5.1,2.5,2.6,3.6,3.4,6.1,7.4,5.2,4.5,5.3,4,4.2,5.4,5.7,3.2,6.3,4.2,4.4,5,4.3,4.2,4.7,4.1,5.4,5.2,4.8,4.9,4.5,3.5,6.9,5.3,3.4,5.2,6.7,6.8,5.6,5.6,6.5,5.1,7,6.4,6.4,7.4,5.8,6.7,5.3,5.4,7.2,5,6.3,7.6,5.9,4.2,4.9,3.1,5.1,5,5.5,3.7,3.2,5,4.8,2.4,4.1,2.4,5.9,4.3,4,5.3,4.3,4,3.9,6.3,5.8,3.9,6,4.4,5.6,6.1,5,2.9,3.4,3.2,4.7,5.1,5.4,4.2,1.9,4.4,4.5,3.6,5.4,3.9,3.4,4.5,6,3.6,4.2,6.8,7.2,6.2,7.5,7.1,6.7,7,6.5,8.4,6.2,5.3,5.3,5.5,7.4,6.9,7.5,6.8,5.1,6.6,6,4.7,5.6,3.6,3.4,4.7,6.6,4.6,4.5,5.5,5.3,5.4,4.8,5.6,6,6.8,3.8,6.7,5.8,2.7,5,4.4,2.2,4.5,2.4,2.7,3.8,4.5,4.5,4.1,3.4,2.4,4.1,5,3.8,3.9,3.4,4.4,2.3,2,4.9,2.4,4.4,3.4,3.9,4.4,6.1,3.9,6.3,4.9,5.9,6,6.5,4,4,5.7,3.6,3.9,6,4.8,6.7,2.8,4.9,5.4,3.9,2.1,3.1,3.5,2.1,5,4.8,2.2,5.1,1.2,4.9,4.8,3,5.7,6.5,6.4,8.1,5.1,4.1,6.3,5.2,7,5.6,6.5,4,7,4.5,6.7,7.5,7,7,5.7,4.6,2.9,4.8,5.8,3.1,4.3,4.1,2.8,5,5.1,4.7,3.4,1.8,4.1,6.1,4.6,3.9,4.8,2.8,6.4,5.6,5.7,5.5,4,5.3,3.7,4.5,3,6,3.6,5.7,5.1,6.1,5.9,4.2,1.6,2.7,3.3,1.4,6.2,5.9,5.6,4.8,5.5,5.5,4.4,7.1,4.3,6.3,8.2,4.4,7.5,5.3,5.9,6.4,5.7,5.1,5.7,6.6,5,4.9,5.4,4.9,5.8,8.4,6.5,4.8,6.7,6,5.2,4.7,5.4,4.7,6.9,5.2,4.8,7.5,4.8,7.7,4.8,5.1,3.4,5.5,4.6,4.8,5.3,4.6,5.4,6.1,5.8,5.5,4.6,6.4,6.5,4.2,4.6,3.1,6.8,7.1,5.5,6.9,4.6,4,6.3,6.9,5.6,8.8,5.7,8.2,8.1,6.6,6.9,5.7,8.8,7.6,9.1,7.7,6,7.4,5.6,8.9,6.4,6,6.6,5.3,6.4,5.6,6.8,5.3,5.1,5.3,6.4,8.5,5.7,5.2,7.5,6.7,7.3,5.1,4.7,5.1,7.4,7.9,7,7.5,6.9,4.5,4,6.2,5.2,7,6.3,5.5,6.6,4.6,5.3,6.4,6.5,7.4,6.7,4.9,5.1,8.6,4.5,5.9,8.1,5.9,6,8.3,5.8,5.5,5.9,8.2,6.9,6.7,6.4,6.4,5.5,7.3,6.7,5.6,7.4,5.3,6.7,6.8,6.5,6.3,5.2,6.8,4.8,7.5,5.8,5.9,6.7,6.3,4.6,4.7,5.5,5.7,4.7,5.2,4,5,5.4,5.3,6.6,5.9,4.1,5.6,5.9,4.7,6.2,4.7,4.9,5.3,6.6,5.1,7.5,7.1,7.1,4.9,4.1,5,4.2,6.5,7.4,5,6.1,4.4,5.6,4.9,5.3,3.1,4.3,5.8,3.1,5.5,5.8,4.9,2.9,4.1,3,5.1,3.6,4,4.9,3.9,4.4,6.9,2.8,5.5,3.7,5.6,5.2,2.6,5.3,4,3.9,1.7,5.8,4.8,6,4.9,5.3,6.3,5.9,5.5,5.6,4.4,7.3,8.4,4.9,4.8,5.7,6,6.1,6.1,6.7,4.5,6.5,5.9,6.9,4,5.8,4.7,6.2,6.7,5.4,5,4.2,5.3,4.4,6.2,3.8,6.3,4.5,5.6,3.3,5.2,4.1,5.1,6.3,6.8,4,6.9,4.8,5.7,4.7,5.1,5.3,3.3,6.6,4.7,4.2,5.9,4.6,6.4,3.8,4.3,5.6,4.4,5.4,8.1,6,7.5,5.8,7.5,7.5,6.4,5.7,6.5,6.8,5.8,7.1,6.4,7.9,8.1,6.6,4,4.5,3.5,5.2,5.5,5,5.1,3.8,6,4,3.2,6.1,4.5,3.6,5.2,4.8,3.9,4.4,6,5.3,5.5,6.1,6.2,2.9,5.6,4.3,6.5,4,3,4.5,3.9,3.8,2.5,3.2,4.3,6.7,4.5,3.7,5.4,5.6,5.6,3.8,6.4,4.4,7.1,4.1,3.9,3.9,5.3,5.2,5.4,5.3,3.7,4.9,6,6.7,5,4,4.7,7.4,4,3.5,4.9,3.2,6.3,6.6,5.5,5.9,4.8,7.4,4.2,5.5,5.9,4,4.3,4.2,5.2,2.7,5.8,4.7,2,4.5,5.4,5.4,3.5,5.3,2.8,5.3,4.6,3.8,3.6,3.7,4.6,3.7,5.6,2.4,4.6,3.9,4.8,6,3.7,4.1,4.5,4.8,3.3,3.9,5.2,4.9,6,2.7,2.7,4.4,4.6,5.3,4.1,4.5,1.4,2.8,2.5,4.2,3.1,1.1,4.2,2.4,0,2.5,1.7,1.9,0.9,1.8,3.6,3.7,4,4.3,1.3,3.2,3.9,5.7,6.3,6.1,5.7,7,5.4,7.6,6.4,5.9,4.5,6,7.1,6.2,6.7,5,7.6,5.3,5.9,5.6,4.9,7.1,8.1,6.2,6.6,6.4,5,5.6,7.5,6.5,5.6,5.3,7.3,6.6,6.2,5.8,7.6,7.1,6.6,4.3,6.8,6,5.1,7.8,7.8,5.5,6.8,5.2,6.4,7.7,6.6,4.7,6.5,7.1,6.3,7,5.4,6.1,6.5,6,7.4,6.7,2.4,5.6,4.7,4.3,4.1,4.6,4.6,3.2,2.2,3,4.3,2.9,5.6,2.9,4.3,5.2,6.2,3.5,3.7,2.9,2,5,2.9,6.1,7,7.3,6.2,6.1,5.4,6.9,4.1,6.1,2,3.5,7.1,6.4,5.9,5.5,5.6,7.7,4.6,4.4,6.4,5.5,3.8,6,5.9,5.7,3.3,5.1,2.7,4.7,4.4,6.4,4.3,3.3,3.1,2.5,5.3,6.2,4.6,5,6.1,4,3.6,3.3,4.5,5.8,5.7,5,5.5,6.9,5.7,6.2,4,3.4,6.8,6,5.4,2,3.2,4.9,5.2,4.1,6.5,4.2,5.4,4.9,4.1,5.1,7.1,3.8,5,6.3,4.9,5.9,6.2,5.2,6.2,7.7,6.5,4.9,5.1,5,5.7,5.3,5.6,4.6,5,5.7,4,4.9,4,7.7,3.8,6.1,4,5.9,5.1,3.5,7.1,5.2,4.8,4.2,5.4,4.4,4.2,3,4,3.8,4.8,4,5,2.1,3.4,5.2,4.8,3.8,5.9,3.5,4,2.8,5.2,5.7,5.1,4.5,4.4,5.9,6.6,3,4,4.3,4.2,5.2,3.3,5.6,6.1,2.8,4.4,3.4,3.6,4.4,4,5.6,6,6.6,6.3,5.7,6.1,5.3,5.7,4.9,4.1,4,6,3.9,4.7,7.2,4.4,4.9,4.1,5,4.1,4.9,3.1,4.1,5.1,5.3,4.5,5.7,7.5,5.3,6.3,5.8,5.9,4.9,3.9,5.4,4.3,6.1,6.7,3.9,5,6.4,7,4.5,4.6,4.4,4.9,7.4,4.9,7.1,5.4,5,6,5,3.2,4.7,4,7.2,4.2,4.3,2.5,2.1,2.8,3.4,3.4,2.9,4.1,3.6,2.2,2.6,3,3.6,1.6,4.9,2.6,6.2,5.5,4.3,3.3,5.8,5.9,4.9,5.3,6.7,6.4,6.1,7.1,4.6,5.7,7.2,8.2,5.6,7.3,6.5,5.5,6.7,6.1,6.8,7.2,6.5,3.4,5.1,3.5,3.8,4.5,4.2,5.3,6.2,5.2,8,4.4,7.4,4.1,5,5.8,4.4,2.9,3.5,5.4,5.9,4.6,4.8,4.2,3.9,3.7,6.1,1.7,5.9,6.1,4.3,3.9,1.1,1.4,1.9,4.9,6.5,3.7,5.2,4.3,2.6,6.7,2.9,5.3],[6,5,6,5,6,5,5,5,5,3,5,5,5,6,5,5,2,3,7,4,6,3,4,4,4,4,5,5,4,4,5,3,4,3,5,4,6,5,3,3,4,6,5,4,3,4,3,5,5,6,6,3,4,5,4,5,6,2,4,5,7,6,7,5,7,6,6,7,5,4,4,5,6,7,6,5,6,5,4,7,6,5,4,5,5,4,5,6,5,5,7,6,6,6,7,4,5,5,5,5,6,5,4,6,4,4,4,4,5,4,4,7,3,5,5,3,5,5,3,5,4,3,5,4,4,2,3,4,3,6,4,6,4,3,4,5,4,4,5,3,4,6,5,6,3,3,5,5,5,3,4,3,4,2,3,3,4,4,3,4,5,5,2,5,5,5,6,7,4,4,4,5,4,4,4,4,3,5,5,6,6,7,4,5,5,3,5,7,6,4,4,6,6,6,5,6,3,3,6,5,4,5,7,6,6,5,5,5,5,5,5,3,5,3,7,5,5,5,6,4,6,4,3,3,5,2,5,4,4,3,5,4,7,4,4,3,5,5,4,2,4,5,4,3,4,5,6,5,6,6,7,7,7,7,6,6,5,7,5,7,7,5,8,6,7,7,3,4,6,3,5,6,2,3,3,4,4,6,4,5,2,6,3,2,4,2,1,6,5,5,8,4,6,6,4,5,6,5,4,6,5,5,4,3,3,5,3,4,5,5,6,5,2,6,4,5,5,6,4,5,4,4,4,5,4,5,5,5,5,5,6,5,6,6,7,3,5,6,5,6,4,6,3,6,6,4,3,5,4,4,6,8,5,6,6,7,6,7,7,7,5,6,7,7,7,8,6,6,6,5,6,8,5,6,7,5,4,5,6,4,6,7,4,6,7,5,6,5,5,6,4,5,6,6,5,5,6,8,5,7,3,3,6,5,5,6,4,5,6,6,5,5,6,5,5,4,4,5,5,5,4,6,6,4,4,7,2,5,6,4,6,6,5,6,6,4,6,7,6,5,5,7,7,5,4,5,7,8,6,7,6,8,6,8,4,6,7,5,7,5,5,5,4,6,5,6,4,6,6,6,6,4,6,4,6,4,3,2,4,5,6,7,4,5,4,5,5,3,3,3,5,6,4,6,4,5,6,5,6,6,4,4,5,4,4,6,5,6,5,4,4,4,4,3,4,5,4,5,4,3,4,6,3,2,3,5,4,4,5,4,2,6,6,6,4,5,3,4,4,5,4,6,4,5,6,4,5,6,4,5,4,5,4,4,5,4,4,4,3,4,7,4,4,6,5,5,6,4,5,5,6,3,6,3,3,4,7,6,5,6,5,6,6,6,6,5,5,4,6,7,6,6,5,4,4,3,3,4,5,4,6,4,4,4,4,4,4,7,6,5,5,7,5,6,4,5,6,6,4,5,3,1,2,4,1,5,1,4,4,6,6,5,7,5,5,4,5,3,4,6,5,6,4,5,4,4,2,5,8,3,4,7,7,8,5,8,7,7,9,7,7,8,10,7,8,6,7,5,8,8,7,4,3,8,5,5,4,4,6,4,5,5,4,5,5,4,4,5,6,5,3,6,5,7,7,9,7,7,8,8,7,7,7,6,7,6,9,8,8,8,5,6,7,6,5,4,4,5,5,4,6,5,6,5,5,4,7,5,7,5,4,4,4,5,8,7,4,6,7,7,5,2,6,4,5,5,5,4,5,7,7,4,4,5,6,6,5,4,4,5,3,2,5,4,5,6,7,4,5,5,4,4,6,5,7,6,7,5,4,5,4,4,5,7,8,4,7,6,7,8,8,7,8,6,4,7,7,7,7,4,5,4,6,5,4,3,1,6,3,3,4,4,4,4,5,2,3,4,4,3,3,4,2,6,8,5,4,5,5,5,5,5,7,5,7,6,5,5,4,6,5,5,5,4,7,4,5,5,6,6,6,4,6,5,6,5,4,5,5,4,5,4,6,5,5,4,5,4,4,5,3,5,5,4,6,6,4,6,4,3,5,7,5,7,6,5,4,7,6,7,6,6,5,5,5,5,6,6,5,5,6,7,3,5,3,6,5,4,5,6,6,5,6,4,5,7,4,5,6,5,5,4,5,5,4,4,5,4,4,6,6,5,6,4,5,4,6,4,6,6,3,5,3,4,2,5,7,2,3,4,3,6,6,4,5,5,4,3,5,6,3,7,4,3,4,4,4,5,5,6,6,3,4,5,3,7,4,4,6,7,7,5,6,6,5,6,6,6,7,6,6,6,7,6,5,6,6,7,5,4,3,6,4,6,5,2,6,4,3,4,4,5,5,4,6,4,3,3,6,6,4,6,4,5,6,5,2,5,3,6,5,6,4,2,4,5,4,7,2,4,4,7,5,4,7,8,6,8,7,6,8,7,7,6,5,5,6,8,7,7,7,6,7,6,4,5,3,4,4,6,5,5,4,5,6,5,5,7,7,4,7,5,3,4,4,2,5,3,3,5,5,3,4,4,3,4,5,4,3,3,4,3,2,5,5,5,4,3,5,6,3,6,4,8,8,5,3,4,5,4,5,6,3,6,3,5,5,5,2,3,2,3,4,6,2,7,2,5,5,3,6,7,5,8,6,4,6,5,7,6,7,5,7,4,7,7,7,7,6,4,4,5,6,3,4,3,3,6,4,6,4,3,4,7,5,4,4,3,7,6,6,5,3,6,5,3,3,5,4,5,6,6,5,5,2,2,6,2,6,5,7,5,5,5,6,7,5,7,7,5,7,7,5,6,5,6,6,7,5,4,4,4,5,6,6,6,6,7,5,5,5,5,7,6,6,6,4,7,5,6,4,5,5,5,6,5,6,6,4,5,5,6,7,3,6,4,6,7,5,6,4,4,6,7,7,8,6,8,8,7,7,6,8,7,8,8,7,7,6,9,7,6,7,6,6,7,6,5,6,5,7,7,6,6,8,5,7,6,5,4,7,7,7,7,8,5,4,6,4,6,7,6,7,5,6,7,6,7,6,4,4,8,4,6,7,5,6,8,5,7,6,9,7,6,6,7,5,6,5,6,7,6,7,7,4,5,6,6,4,7,6,5,7,6,5,5,6,7,5,6,3,6,6,4,6,6,5,5,7,5,5,4,4,4,6,6,7,7,7,4,5,6,4,7,6,5,6,4,7,4,6,5,5,6,4,7,4,5,3,5,4,4,4,5,5,5,5,6,3,5,5,6,7,4,5,5,4,3,5,5,5,5,5,6,5,6,6,4,8,8,5,5,6,5,6,5,6,3,6,5,6,4,5,5,7,7,5,6,4,5,4,6,6,7,6,6,3,6,4,5,6,5,5,5,5,5,5,5,6,5,7,5,4,5,6,6,4,5,6,5,6,8,6,8,6,6,6,7,6,6,7,6,7,6,7,8,6,4,5,4,5,6,4,5,4,6,4,4,4,4,4,4,5,5,5,5,7,5,6,6,3,4,4,6,4,3,5,5,4,3,3,5,6,4,4,5,5,5,4,5,6,7,4,5,4,5,6,7,5,3,5,6,7,6,5,5,7,4,5,6,3,6,6,6,5,5,7,4,6,5,3,5,4,6,3,6,4,2,3,5,5,3,5,3,5,6,5,2,3,5,3,5,2,4,3,5,6,5,4,4,5,4,4,4,3,5,3,3,4,3,4,4,3,1,2,3,4,2,1,3,2,1,3,2,2,1,2,5,4,5,4,1,3,5,6,5,6,5,6,6,6,7,6,5,6,7,7,6,4,8,6,6,6,6,8,7,5,7,7,5,5,9,7,5,5,6,7,6,6,7,7,6,4,7,7,6,8,8,6,7,6,7,7,7,5,8,8,6,7,6,5,6,5,8,7,2,5,4,4,4,5,5,3,2,4,3,2,5,2,5,5,6,3,3,4,2,5,3,6,6,9,7,6,5,7,4,6,3,3,7,6,6,4,6,6,5,5,7,5,4,6,5,5,5,6,2,5,4,4,4,3,4,3,5,5,5,5,5,2,4,5,5,6,5,4,6,7,6,6,3,4,6,5,5,4,4,4,6,5,7,4,5,5,4,5,6,4,6,6,4,7,6,6,6,8,7,5,5,5,6,5,5,6,5,4,4,5,3,6,5,5,4,6,5,3,7,4,4,5,6,4,4,3,4,5,6,4,4,3,3,5,4,5,6,3,4,3,5,5,4,4,4,6,6,4,3,4,6,4,4,6,7,4,5,4,4,4,4,5,6,6,6,6,6,6,6,5,4,4,7,4,4,8,4,5,4,5,5,5,4,5,5,4,6,7,7,5,5,6,6,4,4,5,4,6,6,5,5,6,5,4,5,4,6,7,6,7,4,5,7,6,4,5,4,7,5,4,3,3,3,4,4,3,4,3,2,3,2,3,2,5,2,7,5,5,3,5,6,5,5,6,6,6,6,5,5,6,8,6,7,6,5,6,6,6,7,5,5,5,4,4,6,5,3,6,6,7,4,7,4,5,5,4,4,4,6,5,5,4,4,4,5,7,2,5,7,5,4,1,2,3,6,6,3,4,5,2,7,3,5]],"container":"<table class=\"display\">\n  <thead>\n    <tr>\n      <th> <\/th>\n      <th>pupil<\/th>\n      <th>class<\/th>\n      <th>extrav<\/th>\n      <th>sex<\/th>\n      <th>texp<\/th>\n      <th>popular<\/th>\n      <th>popteach<\/th>\n    <\/tr>\n  <\/thead>\n<\/table>","options":{"columnDefs":[{"className":"dt-right","targets":[1,2,3,5,6,7]},{"orderable":false,"targets":0}],"order":[],"autoWidth":false,"orderClasses":false}},"evals":[],"jsHooks":[]}</script>
]

---

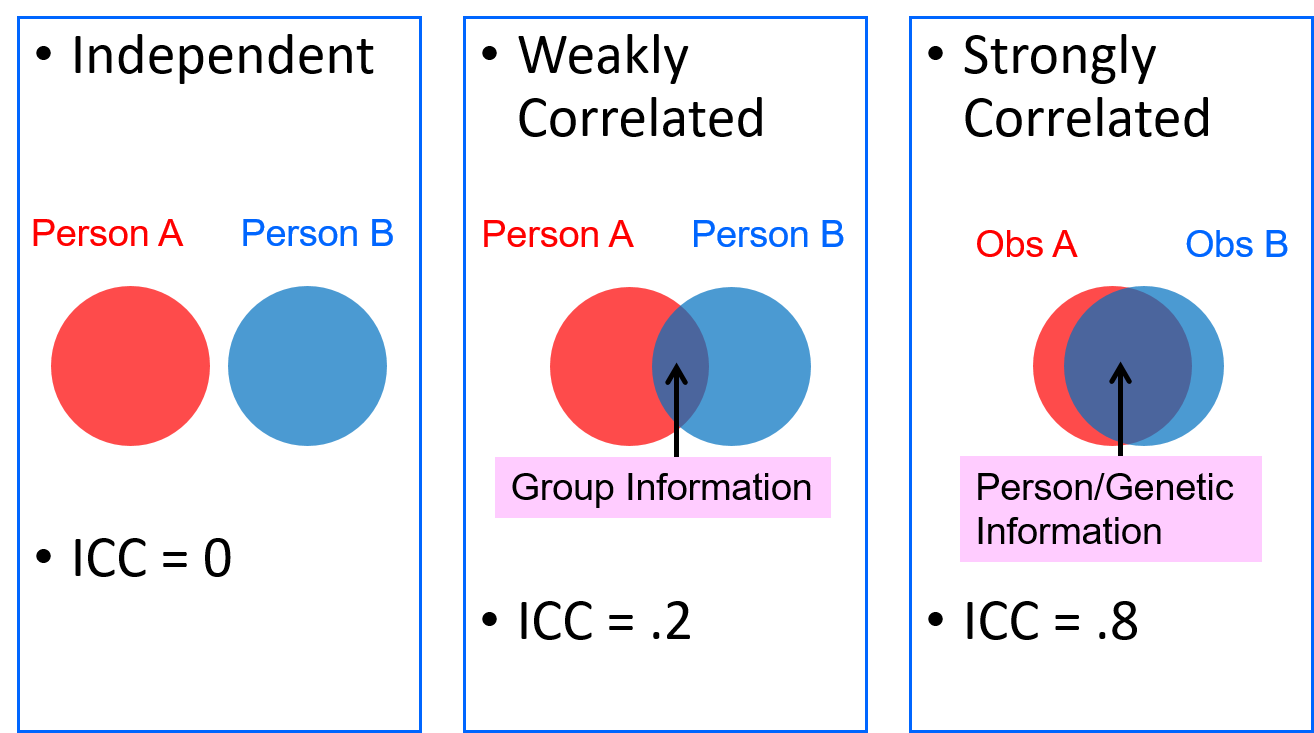
# Intraclass Correlation

---

.right-column[
## Why Use MLM?
- <span style="color:black">Avoid underestimated _SE_</span>
- <span style="color:black">Cluster-specific (or person-specific) regression lines</span>
- <span style="color:black">Avoid Ecological Fallacy</span>
]

---

# Dependent (Correlated) Observations

With clustered data, an assumption of OLS regression is violated

One score informs another score in the same cluster

Overlap: reduces effective information (\$N_\text{eff}\$) in data

???

Two students in the same class give less than two pieces of information

---

# Consequences

Assuming independent obs, OLS understates the uncertainty in the estimates
- _SE_ too small; CI too narrow

`$${\uparrow}\, t = \frac{\hat\beta}{\mathit{SE}(\hat \beta)\, \downarrow}$$`

---

# Comparing OLS with MLM

<div id="htmlwidget-1e2074a54461750d4223" style="width:100%;height:30%;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-1e2074a54461750d4223">{"x":{"diagram":"\ndigraph path1 {\n  graph [layout = neato, fontsize = 24]\n\n  node [shape = rectangle, fontname = \"Helvetica\"]\n  # Schools\n  texp [pos = \"-1,0.5!\"]\n  # Students\n  popular [pos = \"1,-0.5!\"]\n\n  # edges\n  texp -> popular\n}\n","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>

<table cellspacing="0" align="center" style="border: none;">
<tr>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;"><b></b></th>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;"><b>OLS</b></th>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;"><b>MLM</b></th>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">(Intercept)</td>
<td style="padding-right: 12px; border: none;">4.205 (0.071)</td>
<td style="padding-right: 12px; border: none;">4.197 (0.186)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">texp</td>
<td style="padding-right: 12px; border: none;">0.061 (0.005)</td>
<td style="padding-right: 12px; border: none;">0.062 (0.012)</td>
</tr>
<tr>
<td style="border-top: 1px solid black;">Num. obs.</td>
<td style="border-top: 1px solid black;">2000</td>
<td style="border-top: 1px solid black;">2000</td>
</tr>
<tr>
<td style="border-bottom: 2px solid black;">Num. groups: class</td>
<td style="border-bottom: 2px solid black;"></td>
<td style="border-bottom: 2px solid black;">100</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;" colspan="4"><span style="font-size:0.8em"></span></td>
</tr>
</table>
]

---

.pull-left[
![](mlm_intro_recent_advances_files/figure-html/unnamed-chunk-6-1.svg)
OLS:  
95% CI [0.052, 
        0.070]. 
]

.pull-right[
![](mlm_intro_recent_advances_files/figure-html/unnamed-chunk-7-1.svg)
MLM:  
95% CI [0.038, 
        0.085]. 
]

---

# Type I Error Inflation

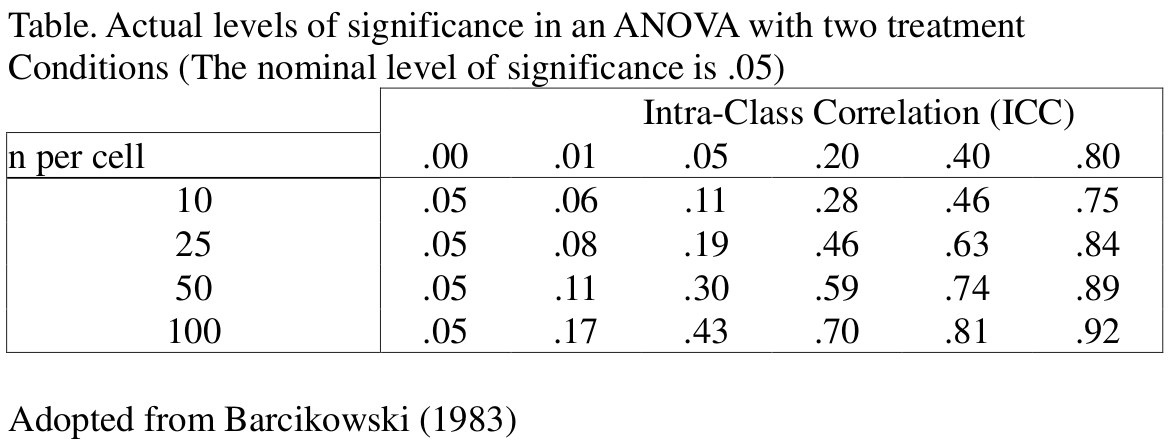
Depends on <span style="color:red">_design effect_</span>: 1 + (cluster size -
1) × ICC

---

Lai and Kwok (2015): MLM needed when __design effect > 1.1__

For the popularity data, design effect  
= 1 + (20 - 1) × .365 = 
7.934

\$N_\text{eff}\$ reduces by almost 8 times: 2000 → 
252
---

.right-column[
## Why Use MLM?
- Avoid underestimated _SE_
- <span style="color:black">Cluster-specific (or person-specific) regression lines</span>
- <span style="color:black">Avoid Ecological Fallacy</span>
]

---

# Random Coefficient Model

Lv-1 predictor: not just problem on _SE_, OLS also ignore potential 
heterogeneity in regression lines

Consider `extrav` --> `popular` (with `extrav` mean centered)
<div id="htmlwidget-c891ad11fabf8f82d20c" style="width:100%;height:25%;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-c891ad11fabf8f82d20c">{"x":{"diagram":"\ndigraph path1 {\n  graph [layout = neato, fontsize = 24]\n\n  node [shape = rectangle, fontname = \"Helvetica\"]\n  # Students\n  extravc [pos = \"-1,0!\"]\n  popular [pos = \"1,0!\"]\n\n  # edges\n  extravc -> popular\n}\n","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>

---

# OLS With All Data

---

# Think About Just One Classroom

`$$\texttt{popular}_i = \beta_0 + \beta_1 \texttt{extrav}_i + e_i$$`

---

# Think About Just One Classroom

`$$\texttt{popular}_{i\color{red}{1}} = \beta_{0\color{red}{1}} + \beta_{1\color{red}{1}} \texttt{extrav}_{i\color{red}{1}} + e_{i\color{red}{1}}$$`

---

# Think About Classroom 35

`$$\texttt{popular}_{i\color{blue}{35}} = \beta_{0\color{blue}{35}} + \beta_{1\color{blue}{35}} \texttt{extrav}_{i\color{blue}{35}} + e_{i\color{blue}{35}}$$`

---

# Classroom 14

`$$\texttt{popular}_{i\color{green}{14}} = \beta_{0\color{green}{14}} + \beta_{1\color{green}{14}} \texttt{extrav}_{i\color{green}{14}} + e_{i\color{green}{14}}$$`

---

### MLM: efficiently get cluster-specific regression lines

`$$\texttt{popular}_{i\color{purple}{j}} = \beta_{0\color{purple}{j}} + \beta_{1\color{purple}{j}} \texttt{extrav}_{i\color{purple}{j}} + e_{i\color{purple}{j}}$$`

---

With heterogeneity in slopes, OLS gives underestimated _SE_ .font60[(Lai and Kwok, 2015)]

.pull-left[
.font80[
Detecting and explaining heterogeneity in slopes (i.e.,
cross-level interaction)
]
]

.pull-right[
<img src="mlm_intro_recent_advances_files/figure-html/unnamed-chunk-11-1.svg" style="display: block; margin: auto;" />
]

---

# Growth Curve Analysis

Individual as "cluster"

---

.right-column[
## Why Use MLM?
- <span style="color:black">Avoid underestimated _SE_</span>
- Cluster-specific (or person-specific) regression lines
- <span style="color:black">Avoid Ecological Fallacy</span>
]

---

# Ecological Fallacy

Association between two variables can be different across levels

<div id="htmlwidget-13245d42a03dda0e2aa2" style="width:100%;height:25%;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-13245d42a03dda0e2aa2">{"x":{"diagram":"\ndigraph path1 {\n  graph [layout = neato, fontsize = 24]\n\n  node [shape = rectangle, fontname = \"Helvetica\"]\n  # Students\n  stu_ach [pos = \"-1.5,0!\", label = \"Student \\nacademic achievement\"]\n  # sch_ach [pos = \"0,-1.5!\", label = \"School average \\nacademic achievement\"]\n  stu_asc [pos = \"1.5,0!\", label = \"Student academic \\nself-concept\"]\n\n  # edges\n  # stu_ach -> sch_ach; \n  stu_ach -> stu_asc [label = \"+ve\"];\n  # sch_ach -> stu_asc;\n}\n","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>

???
students' self-perception in academics
---

# Ecological Fallacy

Association between two variables can be different across levels

<div id="htmlwidget-450e1f1b6f13a4652604" style="width:100%;height:70%;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-450e1f1b6f13a4652604">{"x":{"diagram":"\ndigraph path1 {\n  graph [layout = neato, fontsize = 24]\n\n  node [shape = rectangle, fontname = \"Helvetica\"]\n  # Students\n  stu_ach [pos = \"-1.5,0!\", label = \"Student \\nacademic achievement\"]\n  sch_ach [pos = \"0,-1.5!\", label = \"School average \\nacademic achievement\"]\n  stu_asc [pos = \"1.5,0!\", label = \"Student academic \\nself-concept\"]\n\n  # edges\n  stu_ach -> sch_ach; \n  stu_ach -> stu_asc [label = \"+ve\"];\n  # sch_ach -> stu_asc;\n}\n","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>

---

# Ecological Fallacy

Association between two variables can be different across levels

<div id="htmlwidget-5d94abe86869897365cd" style="width:100%;height:70%;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-5d94abe86869897365cd">{"x":{"diagram":"\ndigraph path1 {\n  graph [layout = neato, fontsize = 24]\n\n  node [shape = rectangle, fontname = \"Helvetica\"]\n  # Students\n  stu_ach [pos = \"-1.5,0!\", label = \"Student \\nacademic achievement\"]\n  sch_ach [pos = \"0,-1.5!\", label = \"School average \\nacademic achievement\"]\n  stu_asc [pos = \"1.5,0!\", label = \"Student academic \\nself-concept\"]\n\n  # edges\n  stu_ach -> sch_ach; \n  stu_ach -> stu_asc [label = \"+ve\"];\n  sch_ach -> stu_asc [label = \"-ve\", color = \"red\", fontcolor = \"red\"];\n}\n","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>

---

# Big Fish Small Fond Effect

Ignoring clustering

---

# Big Fish Small Fond Effect

+ve at student level

---

# Big Fish Small Fond Effect

-ve contextual effect in a more competitive school

---

---

# Recent Advances

---

# Other Forms of Clustering

Three-level

<div id="htmlwidget-db07caa1a13a1eb781a3" style="width:100%;height:35%;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-db07caa1a13a1eb781a3">{"x":{"diagram":"\ndigraph boxes_and_circles {\n  graph [overlap = true, fontsize = 30]\n\n  node [penwidth = 0, fontname = \"Helvetica\"]\n  # District\n  AB [label=\"Therapist 1\"]\n  CD [label=\"Therapist 2\"]\n  # Schools\n  A [label=\"Therapy group A\"]\n  B [label=\"Therapy group B\"] \n  C [label=\"Therapy group C\"]\n  D [label=\"Therapy group D\"]\n  # Students\n  1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11\n\n  # edges\n  edge [dir = \"none\"]\n  AB -> {A; B}\n  CD -> {C; D}\n  A -> {1; 2; 3}\n  B -> {4; 5}\n  C -> {6; 7; 8; 9}\n  D -> {10; 11}\n}\n","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>

---

# Other Forms of Clustering

Cross-classification

<div id="htmlwidget-243497e65e5fdf1cbabe" style="width:100%;height:35%;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-243497e65e5fdf1cbabe">{"x":{"diagram":"\ndigraph boxes_and_circles {\n  graph [overlap = true, fontsize = 30]\n\n  node [penwidth = 0, fontname = \"Helvetica\"]\n  # District\n  n1 [label=\"Neighborhood 1\"]\n  n2 [label=\"Neighborhood 2\"]\n  n3 [label=\"Neighborhood 3\"]\n  # Schools\n  A [label=\"School A\"]\n  B [label=\"School B\"] \n  C [label=\"School C\"]\n  D [label=\"School D\"]\n  # Students\n  1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11\n\n  # edges\n  edge [dir = \"none\"]\n  A -> {1; 2; 3}\n  B -> {4; 5}\n  C -> {6; 7; 8; 9}\n  D -> {10; 11}\n  {1; 4; 5} -> n1\n  {2; 3; 6; 7} -> n2\n  {8; 9; 10; 11} -> n3\n}\n","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>

Partial Nesting

<div id="htmlwidget-52bea27828665ef395c5" style="width:100%;height:25%;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-52bea27828665ef395c5">{"x":{"diagram":"\ndigraph boxes_and_circles {\n  graph [overlap = true, fontsize = 30]\n\n  node [penwidth = 0, fontname = \"Helvetica\"]\n  # Schools\n  A [label=\"Therapy group A\"]\n  B [label=\"Therapy group B\"] \n  C [label=\"Therapy group C\"]\n  D [label=\"Individual therapy\"]\n  # Students\n  1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11\n\n  # edges\n  edge [dir = \"none\"]\n  A -> {1; 2; 3}\n  B -> {4; 5}\n  C -> {6; 7} \n  D -> {8; 9; 10; 11} [style = invis]\n}\n","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>

---

# Effect Size for Multilevel Trials

Effect size (e.g., Cohen's _d_) required by many reporting standards
- Little guidance on how to compute them

---

# Effect Size for Multilevel Trials

Two-level trials: Hedges (2007)

Lai and Kwok (2014): (partially) cross-classified

Lai and Kwok (2016): partially nested

Rights and Sterba (2018): Defining `$R^2$` for MLM

---

# Stice, Shaw, Burton, and Wade (2006)

Eating disorder prevention  
Outcome: Thin-ideal internalization (TII)

.font50[
[Photo](https://www.flickr.com/photos/daniellehelm/3967455172) by [daniellehelm](https://www.flickr.com/photos/daniellehelm/) / [CC BY](https://creativecommons.org/licenses/by/2.0/)
]

---

<div id="htmlwidget-aaebdc25ae3111f2c9be" style="width:100%;height:25%;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-aaebdc25ae3111f2c9be">{"x":{"diagram":"\ndigraph boxes_and_circles {\n  graph [overlap = true, fontsize = 30]\n\n  node [penwidth = 0, fontname = \"Helvetica\"]\n  # Schools\n  A [label=\"Treatment group A\"]\n  B [label=\"Treatment group B\"] \n  C [label=\"Treatment group C\"]\n  D [label=\"Control\"]\n  # Students\n  1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11\n\n  # edges\n  edge [dir = \"none\"]\n  A -> {1; 2; 3}\n  B -> {4; 5}\n  C -> {6; 7} \n  D -> {8; 9; 10; 11} [style = invis]\n}\n","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>

<table>
 <thead>
  <tr>
   <th style="text-align:left;"> Dissonance-based (Treatment) </th>
   <th style="text-align:left;"> Expressive writing (Control) </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> $N^T$ = 114 females </td>
   <td style="text-align:left;"> $N^C$ = 126 females </td>
  </tr>
  <tr>
   <td style="text-align:left;"> 17 groups </td>
   <td style="text-align:left;">  </td>
  </tr>
  <tr>
   <td style="text-align:left;"> $n$ = 6 to 10 </td>
   <td style="text-align:left;">  </td>
  </tr>
  <tr>
   <td style="text-align:left;"> ICC = .08, $\mathit{deff}$ = 1.5 </td>
   <td style="text-align:left;">  </td>
  </tr>
</tbody>
</table>

---

`$\hat \beta_\text{TREAT}$` = -0.44, _SE_ = 0.09<sup>[1]</sup>

How many *SD*s does that correspond to?

.footnote[
[1] OLS underestimates _SE_ by 25%; falsely assuming full clustering
underestimates _SE_ by 15%.
]

---

# Lai and Kwok (2016)

`$$\hat \delta = \frac{\hat \beta_\text{TREAT}}{\hat \sigma^2_\text{person}}$$`

`$$V(\hat \delta) = \frac{V(\hat \beta_\text{TREAT})}{\hat \sigma^2_\text{person}} + 
                   \frac{\hat \delta^2 V(\hat \sigma^2_\text{person})}{4 (\hat \sigma^2_\text{person})^2}$$`
                   
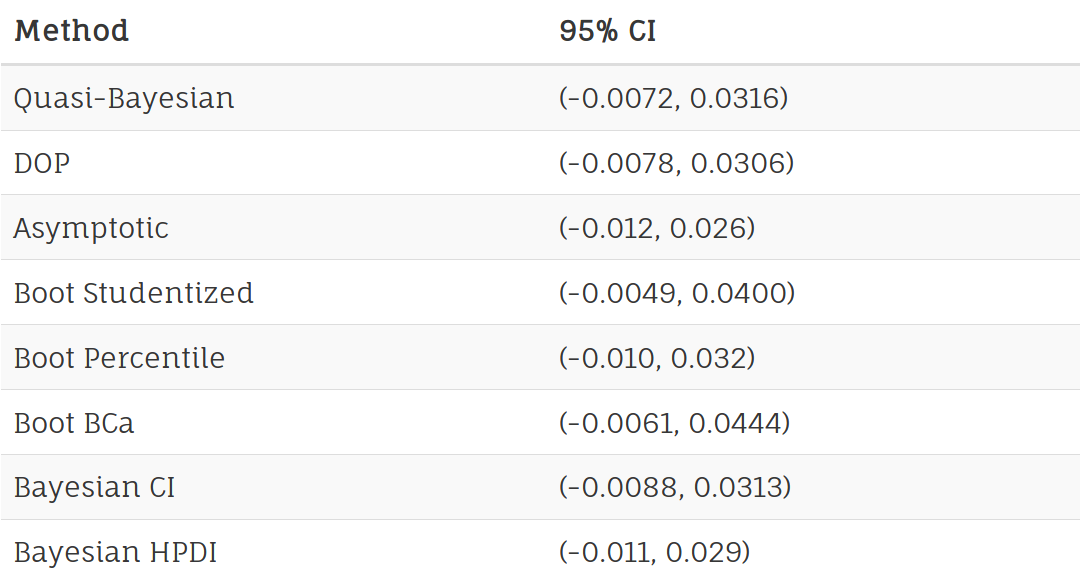
For Stice, Shaw, Burton, et al. (2006), `$\hat \delta$` = -0.98, 95% CI = [-1.4, -0.6]

---

# Multilevel Bootstrapping

Useful for
- CI for effect size
- testing multilevel mediation

`bootmlm` R package .font60[(Lai, 2018)]:
currently implements 6 flavors of bootstrapping and 5 types of CI estimates

---

<div id="htmlwidget-01297a146c5210c9a4eb" style="width:100%;height:25%;" class="grViz html-widget"></div>
<script type="application/json" data-for="htmlwidget-01297a146c5210c9a4eb">{"x":{"diagram":"\ndigraph path1 {\n  graph [layout = neato, fontsize = 24]\n\n  node [shape = rectangle, fontname = \"Helvetica\"]\n  # Students\n  free [pos = \"-1.5,0!\", label = \"School \\npoverty\"]\n  smorale [pos = \"0,0!\", label = \"School \\nmorale\"]\n  late [pos = \"1.5,-1!\", label = \"Student \\ntardiness\"]\n\n  # edges\n  free -> smorale\n  free -> late\n  smorale -> late\n}\n","config":{"engine":"dot","options":null}},"evals":[],"jsHooks":[]}</script>

---

# Accounting for Survey Design

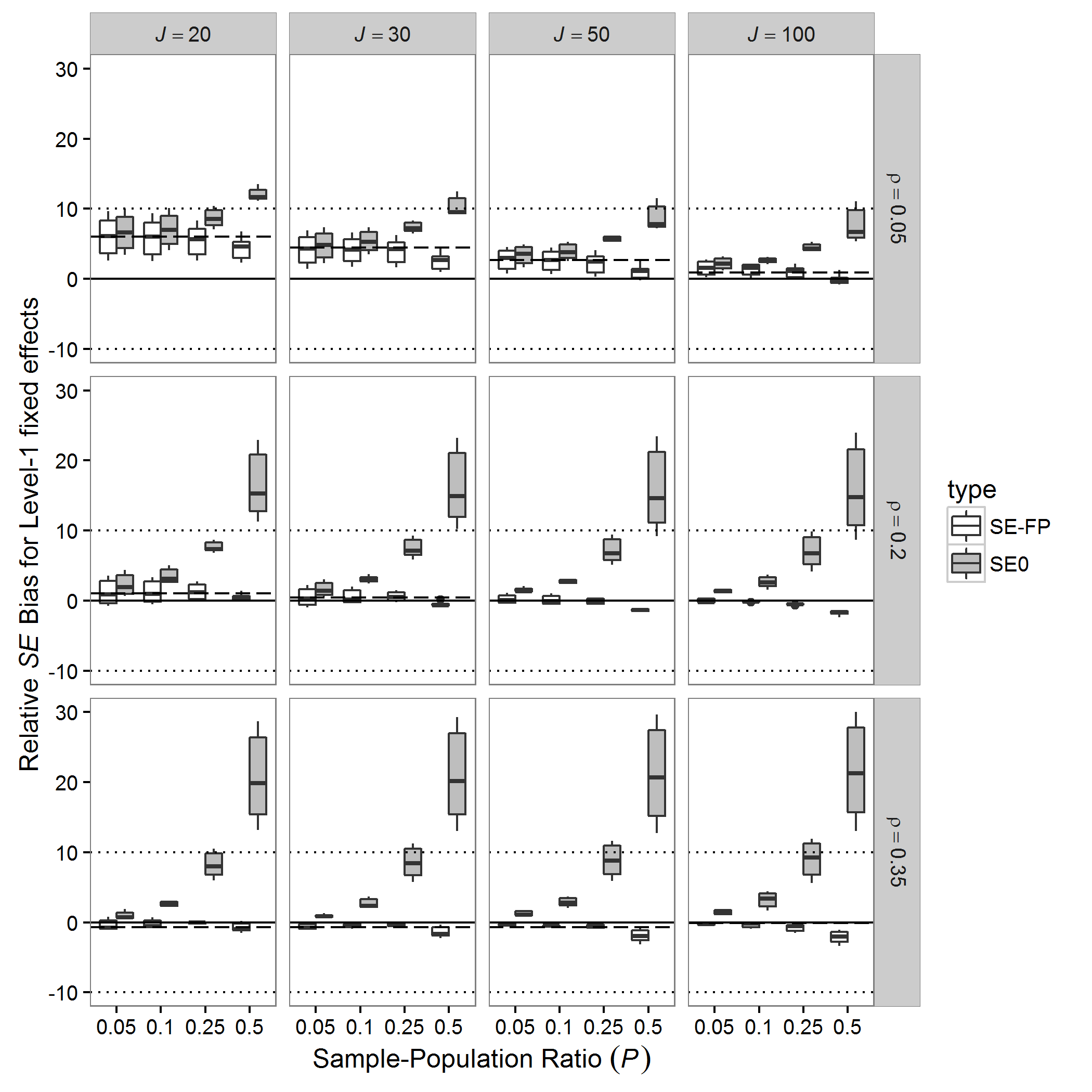
Lai, Kwok, Hsiao, and Cao (2018)
- Apply finite population correction for cross-cultural research to obtain
more accurate _SE_ (and improved power)

Wen & Lai (in preparation)
- A multilevel Bayesian semi-parametric bootstrap procedure to handle sampling 
weights with unequal probability samples

---

---

# MLM of Non-Normal Outcomes

Ordinal? Counts? Zero-inflated? Proportions? Response time? Survival?

These are made easy with Bayesian estimation and the `brms` package 
.font60[(Bürkner, 2018)].

---

# Final Remarks

Reasons for MLM: correct _SE_, model heterogeneity, avoid ecological fallacy

Methodological research: translate methods in single-level research + methods
for new RQ

More truly multilevel theories

---

# Bibliography

.font70[
Aitkin, M. and N. Longford (1986). "Statistical modelling issues
in school effectiveness studies". In: _Journal of the Royal
Statistical Society. Series A (General)_ 149, pp. 1-43. DOI:
[10.2307/2981882](https://doi.org/10.2307/2981882).

Bürkner, P. (2018). "Advanced Bayesian Multilevel Modeling with
the R Package brms". In: _The R Journal_ 10.1, pp. 395-411.

Hedges, L. V. (2007). "Effect sizes in cluster-randomized
designs". In: _Journal of Educational and Behavioral Statistics_
32, pp. 341-370. DOI:
[10.3102/1076998606298043](https://doi.org/10.3102/1076998606298043).

Hox, J. J, M. Moerbeek and R. Van de Schoot (2018). _Multilevel
analysis: Techniques and applications_. 3rd ed. New York, NY:
Routledge.
]

---

.font70[
Lai, M. H. C. (2018). _marklhc/bootmlm: bootmlm: bootstrap
resampling for multilevel models_. DOI:
[10.5281/zenodo.1879127](https://doi.org/10.5281/zenodo.1879127).

Lai, M. H. C. and O. Kwok (2014). "Standardized mean differences
in two-level cross-classified random effects models". In: _Journal
of Educational and Behavioral Statistics_ 39.4, pp. 282-302. DOI:
[10.3102/1076998614532950](https://doi.org/10.3102/1076998614532950).

Lai, M. H. C. and O. Kwok (2015). "Examining the rule of thumb of
not using multilevel modeling: The “design effect smaller than
two” rule". En. In: _The Journal of Experimental Education_ 83.3,
pp. 423-438. DOI:
[10.1080/00220973.2014.907229](https://doi.org/10.1080/00220973.2014.907229).

Lai, M. H. C. and O. Kwok (2016). "Estimating standardized effect
sizes for two- and three-level partially nested data". In:
_Multivariate Behavioral Research_, pp. 1-17. DOI:
[10.1080/00273171.2016.1231606](https://doi.org/10.1080/00273171.2016.1231606).

Lai, M. H. C, O. Kwok, Y. Hsiao, et al. (2018). "Finite population
correction for two-level hierarchical linear models.". In:
_Psychological Methods_ 23.1, pp. 94-112. DOI:
[10.1037/met0000137](https://doi.org/10.1037/met0000137).
]

---

.font70[
Leeuw, J. de and I. Kreft (1986). "Random coefficient models for
multilevel analysis". In: _Journal of Educational Statistics_ 11,
pp. 57-85. DOI:
[10.2307/1164848](https://doi.org/10.2307/1164848).

Littell, R. C, G. A. Milliken, W. W. Stroup, et al. (1996). _SAS
System for mixed models_. Cary, NC: SAS.

Raudenbush, S. W. and A. S. Bryk (2002). _Hierarchical linear
models: Applications and data analysis methods_. 2nd ed. Thousand
Oaks, CA: Sage.

Rights, J. D. and S. K. Sterba (2018). "Quantifying explained
variance in multilevel models: An integrative framework for
defining R-squared measures.". In: _Psychological Methods_. ISSN:
1939-1463. DOI:
[10.1037/met0000184](https://doi.org/10.1037/met0000184).

Stice, E, H. Shaw, E. Burton, et al. (2006). "Dissonance and
healthy weight eating disorder prevention programs: A randomized
efficacy trial.". In: _Journal of Consulting and Clinical
Psychology_ 74, pp. 263-275. DOI:
[10.1037/0022-006X.74.2.263](https://doi.org/10.1037/0022-006X.74.2.263).
]

---

# Thanks!

Slides created via the R package [**xaringan**](https://github.com/yihui/xaringan).

---

# Fixed Effect Estimates

<table cellspacing="0" align="center" style="border: none;">
<tr>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;"><b></b></th>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;"><b></b></th>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">(intercept)</td>
<td style="padding-right: 12px; border: none;">5.031 (0.097)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">extravc</td>
<td style="padding-right: 12px; border: none;">0.493 (0.025)</td>
</tr>
<tr>
<td style="border-top: 1px solid black;">Var(intercept)</td>
<td style="border-top: 1px solid black;">0.892</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Var(slope)</td>
<td style="padding-right: 12px; border: none;">0.026</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Cov(int, slope)</td>
<td style="padding-right: 12px; border: none;">-0.134</td>
</tr>
<tr>
<td style="border-bottom: 2px solid black;">Var(residual)</td>
<td style="border-bottom: 2px solid black;">0.895</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;" colspan="3"><span style="font-size:0.8em"></span></td>
</tr>
</table>
]

Average slope of `extrav` = 0.493, 95% CI 
[0.442, 0.543].

---

# Random Effect __Variance__ Estimates

<table cellspacing="0" align="center" style="border: none;">
<tr>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;"><b></b></th>
<th style="text-align: left; border-top: 2px solid black; border-bottom: 1px solid black; padding-right: 12px;"><b></b></th>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">(intercept)</td>
<td style="padding-right: 12px; border: none;">5.031 (0.097)</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">extravc</td>
<td style="padding-right: 12px; border: none;">0.493 (0.025)</td>
</tr>
<tr>
<td style="border-top: 1px solid black;">Var(intercept)</td>
<td style="border-top: 1px solid black;">0.892</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Var(slope)</td>
<td style="padding-right: 12px; border: none;">0.026</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;">Cov(int, slope)</td>
<td style="padding-right: 12px; border: none;">-0.134</td>
</tr>
<tr>
<td style="border-bottom: 2px solid black;">Var(residual)</td>
<td style="border-bottom: 2px solid black;">0.895</td>
</tr>
<tr>
<td style="padding-right: 12px; border: none;" colspan="3"><span style="font-size:0.8em"></span></td>
</tr>
</table>
]

Variance of slopes = 0.026 (_SD_ = 0.161)
- For a majority of schools (within +/- 1 _SD_), slope expected in the range
[0.332, 0.654].

???
for linear relations, only need to know the intercept and the slope;