本文主要介绍p-curve分析的基本原理，p-curve分析的基本步骤，如何在文献中报告p-curve结果，以及p-curve在元分析中的应用。

p-curve的原理简介

The p-curve is a plot of the distribution of p-values reported in a set of scientific studies. [@bishop_problems_2016]p-curve 是一组科学研究中报告的 p 值分布。

The term p-hacking was introduced by Simonsohn, Nelson & Simmons (2014) to describe the practice of reporting only that part of a dataset that yields significant results, making the decision about which part to publish after scrutinising the data. There are various ways in which this can be done: e.g., deciding which outliers to exclude, when to stop collecting data, or whether to include covariates.
p-hacking这一术语由Simonsohn，Nelson＆Simmons (2014)引入，用于描述仅报告产生显著结果的数据的做法，在对数据进行审查后作出决定哪部分用来进行发表。 有多种方法可以做到这一点：例如，决定要排除哪些异常值，何时停止收集数据，或者是否包括协变量。

Simonsohn, Nelson & Simmons (2014) proposed a method for diagnosing p-hacking by considering the distribution of p-values obtained over a series of independent studies. Their focus was on the p-curve in the range below .05, i.e., the distribution of probabilities for results meeting a conventional level of statistical significance. The logic is that a test for a group difference when there is really no effect will give a uniform distribution of obtained p-values. In contrast, when there is a true effect, repeated studies will show a right-skewed p-curve, with p-values clustered at the lower end of the distribution (see Fig. 1). As shown by Simonsohn, Nelson & Simmons (2014), the degree of right skew will be proportional to sample size (N), as we have more power in the study to detect real group differences when N is large (Cohen, 1992).

P curve analyzes the distribution of p values among published articles to distinguish whether the findings provide evidence for a true phenomenon, or whether they likely reflect an arti- fact of publication bias and p hacking. This reasoning is based on evidence that studies demonstrating true effects (where the null is false) will be more likely to produce particularly low p values (ps < .025) than will p values in the higher range of significance (.025 < ps < .05; Lehmann, 1986; Wallis, 1942). The distribution of p values (the “p curve”) for a true effect should thus be right-skewed. Studies that are investigating null effects will produce an equal dis-tribution of p values, resulting in a uniform p curve. This type of “flat” p curve suggests that the body of literature lacks evidentiary value. [@shariff_religious_2016]

p-curve 通过分析已发表的研究中的p值分布情况，鉴别这些研究发现是否为真实现象提供证据价值，或者是否反映了出版偏差以及 p hacking^[这一术语由Simonsohn，Nelson＆Simmons (2014)引入，用于描述仅报告产生显著结果的数据的做法，在对数据进行审查后作出决定哪部分用来进行发表。 有多种方法可以做到这一点：例如，决定要排除哪些异常值，何时停止收集数据，或者是否包括协变量]。 这种推理是基于证据表明真实效应（null为假）的研究将更有可能产生特别低的p值（ps <.025），而不是p值在较高的显着性范围内（0.025 < ps < .05; Lehmann，1986; Wallis，1942）。 因此，存在真实效应时的p值的分布（“p曲线”）应该是右偏的(right-skewed)。 而那些零效应的研究将产生均匀分布的p曲线。 这种“平坦”的p曲线表明，这些研究缺乏证据价值。

P-curve analysis thus tests the skew of the distribution of p values for a given set of studies and can detect evidential value even with a small number of under-powered studies. As recommended in Simonsohn et al. (2014), a detailed disclosure table reports the hypotheses, results, and p values of all included studies selected, as well as details on how any ambiguous decisions were resolved (Table S2 in online supplemental materials).

因此，P曲线分析通过检验给定的一组研究的p值分布的偏态性，可以检测该组研究的证据价值（即使在少量的低统计检验力的研究中）。 根据Simonsohn等人（2014）的建议 ，详细的公开表（a detailed disclosure）报告了所选择的研究中的假设，结果和p值，以及如何解决任何不明确的决定的细节。

当虚无假设H0为真时，p 值应该是在0－1之间均匀分布的。而当真实效应H1为真时，一个统计检验力比较强的实验中，p值的分布是靠近0这一端，而且是在小于0.01这一端比较多，即p-curve应呈右偏态分布（见下图）。

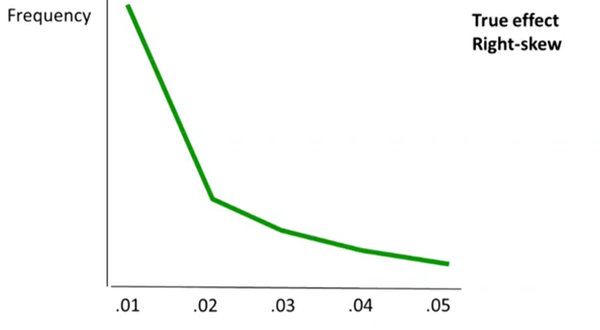
基于上述理论假设，假如一个研究的效应是真实的（H1为真），那么它的P值应该更多分布在小的一端（0.01），而不是0.05这一端。所以，如果我们找出一系列关于这个效应的研究，把他们的阳性结果(p< 0.05)的p值拿来做一个分布，看看是更多地靠近0.05，还是0.01。如果靠近0.01，则更有可能是在H1为真的情况下的数据（比如下图的教授启动效应）。

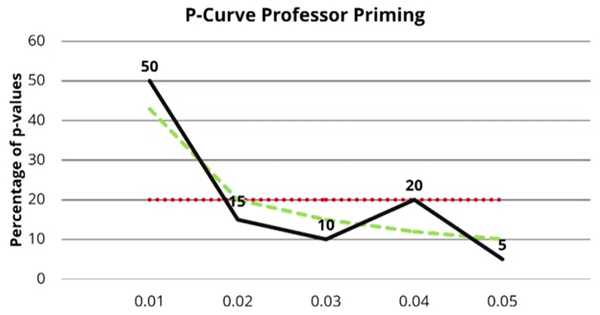
检验p-curve是否为右偏态：二项检验比较p<0.25和p>0.25的概率，连续检验计算pp值：虚无假设成立的前提下得到小于该值的概率均匀分布时，pp=p/.05；使用Stouffer方法检验其是否右偏态（虚无假设为均匀分布）。

P-Curve analysis report using in English papers

The p-curve is a plot of the distribution of p-values reported in a set of scientific studies. Simonsohn, Nelson & Simmons (2014) proposed a method for diagnosing p-hacking by considering the distribution of p-values obtained over a series of independent studies. P-curve analyzes the distribution of p values among published articles to diagnose whether the findings provide evidence for a true phenomenon, or whether they likely reflect an artifact of publication bias and p hacking. The logic is that studies demonstrating true effects (where the null is false) will be more likely to produce particularly low p values (ps < 0.025) than will p values in the higher range of significance (0.025 < ps < 0.05). The distribution of p values (the “p curve”) for a true effect should thus be right-skewed. Studies that are investigating null effects will produce an equal distribution of p values, resulting in a uniform p curve. This type of “flat” p curve suggests that the body of literature lacks evidentiary value (Shariff, Willard, Andersen, & Norenzayan, 2016).

Official User-Guide to the P-curve

[@simonsohn_p-curve_2014]提供了一个网页的 App方便研究者计算p-curve，如果你熟悉 R 的话，也可以直接在 R 软件中计算p-curve。

Four steps to a valid p-curve:

1. Create and report a study-selection rule 
创建和报告研究选择的标准，例如：The yearly top-5 most cited articles in the Quarterly Research Journal 1984-1989

2. Create a P-curve Disclosure Table to select results to analyze 
创建P-curve公开表选择结果进入分析 Keep in mind: In a 2x2 design, o If attenuation is predicted, select only the interaction 如果是衰减型的交互作用，只选择交互作用的统计值
o If a reversal is predicted, select only both simple effects 如果

3. Feed statistical results to p-curve app 
把统计结果提供给p-curve app 。You can copy paste your tests in the format used in the examples there.
If you have results p>.05, the app will automatically exclude them and report how many were excluded.

4. Copy-paste app’s output onto your paper 
拷贝相关结果

p-curve结果的解释 (P-CURVE RESULTS - App 4.052)

Interpretation:

P-Curve analysis combines the half and full p-curve to make inferences about evidential value. In particular, if the half p-curve test is right-skewed with p<.05 or both the half and full test are right-skewed with p<.1, then p-curve analysis indicates the presence of evidential value. This combination test, introduced in Simonsohn, Simmons and Nelson (2015 .pdf) ‘Better P-Curves’ paper, is much more robust to ambitious p-hacking than the simple full p-curve test is. p-curve分析结合一半或全部p-curve进行证据价值的推断。当一半p-curve检验是右偏时p<.05 ，或者一半和全部p-curve是右偏时p<.1，p-curve分析表明存在证据价值。这种联合检验，由Simonsohn, Simmons and Nelson (2015 .pdf) 引入，对极端的p-hacking检验更为稳定。

Similarly, p-curve analysis indicates that evidential value is inadequate or absent if the 33% power test is p<.05 for the full p-curve or both the half p-curve and binomial 33% power test are p<.1. Here neither condition is met; so p-curve does not indicate evidential value is inadequate nor absent. 类似地，p曲线分析表明，如果33％检验力测试对于整个p曲线为p <.05，或者半数p-curve和二项式33％功率测试均为p <.1，则表明证据值不足或不存在。 这里两者都不符合条件; 所以p曲线并不表示证据价值不足或不存在。

As with all p-values, these cutoffs are just benchmarks; the lower the p-values are, the less consistent the data are with the respective null hypotheses. A p=.049 is essentially the same as a p=.051, while a p=.0001 is much more compelling than either. 与所有p值一样，这些截止值只是基准; p值越低，数据与相应的零假设越不一致。 p = 0.049与p = 0.051基本相同，而p = 0.0001比任一者更强烈。

Brief Explanations of Main Results:

1. Binomial tests compare the observed proportion of significant results that are p<.025 (in this case: 88%) to the expected proportions when there is no effect (50%), and when studies have 1/3 power (71%). This latter number varies (by a few %s) as a function of the degrees of freedom of the tests submitted to p-curve. 二项式检验将观察到p <.025的显着结果（在这种情况下为88％），与无效应（50％）的预期，以及与1/3功率（71％）比例相比较。 后一个变量随着提交给p曲线的测试的自由度而变化。

2. Continuous tests are obtained by computing pp-values for each test (probability of at least as extreme a p-value conditional on p<.05), and converting them to Z scores(N(0,1)). The sum of these Z scores (8 in this case), divided by the square-root of the number of tests included (again: 8 in this case) is the reported Z score in that column (and corresponding p-value). This approach is known as Stouffer’s Method. (Prior to App 3.0 we relied on Fisher’s method instead. See “Better P-Curves” paper.) 连续测试通过计算每个测试的pp值（至少与p <.05有关的p值的极限概率）并将其转换为Z分数（N（0,1））获得。 这些Z分数的总和（在这种情况下为8）除以包括的测试次数的平方根（在这种情况下，再次为8）是该列中报告的Z分数（和相应的p值）。 这种方法被称为Stouffer方法。 （在App 3.0之前，我们依靠Fisher的方法，参见“更好的P曲线”）。 Note that the binomial and continuous tests are by definition one-sided (e.g., more right skewed than flat). We use negative Z values to indicate deviation in the direction of the alternative hypothesis of interest; for example a negative Z value for the Right-Skew test is evidence against the flat null, and thus in favor of Right-Skew. 注意，二项式和连续测试的定义是单项的（例如，相对于平坦，更右偏向）。 我们使用负的Z值来表示与感兴趣的替代假设方向的偏差; 例如右偏试验的负Z值是针对不平坦的证据，因此有利于右倾。

3. Statistical power is obtained by comparing the expected p-curve for each possible value of power between 5% and 99% to the observed p-curve, and selecting the level of power that leads to the expected p-curve that most closely resembles the observed p-curve. (We quantify the similarity with the overall Z arising from aggregating the resulting pp-values via the Stouffer method, pp-values which depend on the assumed level of power). The best fit possible is Z=0. 统计功率通过将观察到的p曲线的5％至99％之间的每个可能的功率值与预期p曲线进行比较来获得，并且选择导致与观察到的非常类似的预期p-曲线的功率水平。（我们量化与通过Stouffer方法聚集所得到的pp值产生的整体Z的相似度，其取决于假定的功率水平）。 最佳拟合可能是Z = 0。

Explaining these calculations with an example:

Take the first significant result entered: t(88)=2.1. It is associated with a two-sided p-value of 0.03859. pp-values are the probability of at least as extreme a significant p-value. For right skew we compute these under the null of no effect; because p-values would be distributed uniform between 0 and .05, we simply divide by .05 (multiply by 20) and get the pp-value for right skew, that is 0.03859*20=0.77182. One minus that gives us the pp-value for left skew (not shown above). 取第一个显着的结果输入：t（88）= 2.1。 它与双面p值0.03859相关联。 pp值是至少与极值p值有关的概率。 对于正确的偏移，我们在无效的空值下进行计算; 因为p值在0和.05之间是分布均匀的，所以我们只需要除以.05（乘以20），得到正确偏移的pp值，即0.03859 * 20 = 0.77182。 一个减去给我们左偏移的pp值（未显示在上面）。

For the pp-value under the null that the test is powered to 33% things are a bit more complicated. This explanation will not be quite enough, but: we find the non-centrality parameter for the corresponding distribution and degrees of freedom that gives 33% power. We then evaluate in that non-central distribution the observed test statistic, t(88)=2.1, and now divide by 33% rather than 5% because now 1/3 of tests are expected to be p<.05 rather than only 5% of them. 对于在null下的pp值，测试被提供给33％的东西有点复杂。这个解释是不够的，但是我们发现相应分布和自由度的非中心参数为33％。然后，我们在非中心分布中评估观察到的测试统计量t（88）= 2.1，现在除以33％而不是5％，因为现在1/3的测试预期为p <.05而不是仅5 ％的他们。

More importantly, the interpretation of the pp-value for 33% power is as follows. If the underlying effect size were big enough to give the sample of the study obtaining t(88)=2.1 33% power, then with probability 0.11764 we would get a p-value of 0.03859 or higher. 更重要的是，pp值的解释为33％的权力如下。如果基本效应大小足够大，使得研究样本获得t（88）= 2.1 33％的幂，则以0.11764的概率得到0.03859或更高的p值。

For the half p-curve we proceed similarly. First, for right skew we divide by .025 (multiply by 40). When a p-value is >.025 it is not included in half p-curve, we see “NA” in the table above. For 33% power, in turn, we use the same non-centrality parameter but this time we divide by the share of p-values expected to be p<.025 when power is 33%. 对于半p曲线，我们进行类似的操作。首先，对于正确的偏移，我们除以.025（乘以40）。当p值为.025时，它不包含在半对数曲线中，我们在上表中看到“NA”。对于33％的功率，反过来，我们使用相同的非中心参数，但是这次我们除以预期为p <.025的p值的份额，当功率为33％时。

The last four columns report the Z-Scores associated with those pp-values. So for the full p-curve right-skew pp-value we had pp=0.77182. Evaluating the standard normal distribution in that percentile gives us the reported Z=0.74. 最后四列报告与这些pp值相关联的Z-Scores。 因此，对于完整的p曲线右偏斜pp值，我们得到pp = 0.77182。 评估该百分位数中的标准正态分布给出了报告的Z = 0.74。

Diagnostic plot for power estimation

This figure plots how consistent the observed p-curve is with each possible value of power between 5% and 99%. To create the figure we compute pp-values for the null that all studies are powered with a given level of power and combine those pp-values using Stouffer’s method. The best fitting level of power will lead to an overall Stouffer Z=0, p=.5. 该图表示观察到的p曲线与5％至99％之间的每个可能的功率值的一致性。 为了创建这个数字，我们计算所有研究的pp值为一个给定的幂级数，并使用Stouffer方法组合这些pp值。最佳拟合水平的电力将导致整体Stouffer Z = 0，p = 0.5。

This approach is different from the one used with App 3.0 where instead the Kolmogorov-Smirnov test was run on the resulting distribution of pp-values and the uniform. The results with both methods are very similar. The main advantage of the KS test approach is that it reports absolute fit between expected and observed p-curve. The main advantage of the Stouffer method is that it is the approach used to compute the confidence interval and is hence more parsimonious. The table with results at the top of this page reports 73% as the estimate of power. This means that if all studies in the set were truly powered to 73%, half the time we would see a flatter p-curve than the one we see, and half the time we would see a more right-skewed one. So 73% is our best guess. 这种方法与App 3.0中使用的方法不同，而是在所得到的pp值和均匀分布上进行Kolmogorov-Smirnov测试。两种方法的结果非常相似。 KS测试方法的主要优点是报告了预期和观察到的p曲线之间的绝对匹配。 Stouffer方法的主要优点在于它是用于计算置信区间的方法，因此更加节省时间。 本页顶部的结果表显示了73％的功率估算值。这意味着如果所有的研究都是真正的73％的研究，那么一半的时间我们会看到比我们看到的更为平坦的p曲线，而一半的时间我们会看到一个更偏向的。所以73％是我们最好的猜测。

p-curve在元分析中的应用

评估发表偏差和p-hacking

Selecting p Values [@simonsohn_p-curve:_2014]

Most studies report multiple p values, but not all p values should be included in p-curve. Included p values must meet three criteria: (a) test the hypothesis of interest, (b) have a uniform distribution under the null, and (c) be statistically independent of other p values in p-curve. Here, we propose a five-step process for selecting p values that meet these criteria (see Table 1). 大多数研究报告多个p值，但并不是所有p值都应该包含在p曲线中。 包含的p值必须满足三个标准：（a）测试感兴趣的假设，（b）在null下均匀分布，（c）统计学上与p曲线中的其他p值无关。 在这里，我们提出了一个五步法来选择符合这些标准的p值（见表1）。

An example form @shariff_religious_2016

As p curve is a new tool, we will briefly explain the logic behind the analysis. We refer interested readers to the original paper (Simonsohn et al., 2014) for more details. P curve analyzes the distribution of p values among published articles to distinguish whether the findings provide evidence for a true phenomenon, or whether they likely reflect an artifact of publication bias and p hacking. This reasoning is based on evidence that studies demonstrating true effects (where the null is false) will be more likely to produce par- ticularly low p values (ps < .025) than will p values in the higher range of significance (.025 < ps < .05; Lehmann, 1986; Wallis, 1942). The distribution of p values (the “p curve”) for a true effect should thus be right-skewed. Studies that are investigating null effects will produce an equal dis- tribution of p values, resulting in a uniform p curve. This type of “flat” p curve suggests that the body of literature lacks evidentiary value. The use of QRPs to pull findings below the threshold of statistical significance—when there is no real effect—is more likely to produce p values in the upper range of significance (e.g., .04 < ps < .05). A set of studies overwhelmingly composed of p-hacked effects but that actually lacks evidentiary value will thus likely produce a left-skewed p curve. P-curve analysis thus tests the skew of the distribution of p values for a given set of studies and can detect evidential value even with a small number of under- powered studies. As recommended in Simonsohn et al. (2014), a detailed disclosure table reports the hypotheses, results, and p values of all included studies selected, as well as details on how any ambiguous decisions were resolved (Table S2 in online supplemental materials).

由于p曲线是一个新工具，我们将简要解释其背后的逻辑。感兴趣的读者可以到其原始论文 (Simonsohn et al., 2014) 中了解更多细节。 P曲线通过分析已发表的研究中p值的分布情况，鉴别这些研究发现是否为真实现象提供证据价值，或者是否反映了出版偏差以及 p hacking^[这一术语由Simonsohn，Nelson＆Simmons (2014)。这种推理是基于证据表明真实效应（null为假）的研究将更有可能产生特别低的p值（ps <.025），而不是p值在较高的显着性范围内（0.025 <ps < .05; Lehmann，1986; Wallis，1942）。 因此，存在真实效应时的p值的分布（“p曲线”）应该是右偏的(right-skewed)。 而那些零效应的研究将产生均匀分布的p曲线。 这种“平坦”的p曲线表明，这些研究缺乏证据价值。因此，P曲线分析通过检验给定的一组研究的p值分布的偏态性，可以检测该组研究的证据价值（即使在只有少量的低统计检验力的研究情况下）。

Selection of articles. P curve aims to test the distribution of p values in the full record of published research. As a result, the inclusion criteria for p-curve analyses exclude all unpub- lished studies and all studies that resulted in effects that did not reach p < .05. Because studies that result in p values more than .05 are only selectively reported, with some published and most file-drawered, they are not representative of a full distribution. However, we can be confident that studies with p values less than .05 will find their way into journals; thus, the publication record largely represents the full distribution. Eliminating unpublished and p > .05 studies3 from our initial list in Analysis 1 left 66 studies. Adding Study 2 from Ran- dolph-Seng and Nielsen (2007), which was excluded from Analysis 1 but is viable for p curve, brings this total to 67 studies (N = 6,949).

P曲线旨在测试已发表研究中的p值的分布。 因此，p-曲线分析的纳入标准不包括所有未发表的研究和所有未达到p <.05的研究。 因为导致p值超过0.05的研究只能有选择性地报告，一些已发表和大多数档案提取的研究报告并不代表完整分布。 然而，我们相信，p值小于0.05的研究终将进入期刊发表; 因此，出版的记录在很大程度上代表了全面的 p 值分布。 排除未发布和p> .05的研究最后剩下66项研究。加上研究2中的一项实用于p曲线分析的研究，总共得到67项研究（N = 6,949）。

Selection of analyses. In addition to choosing studies, p curve also requires the selection of the specific p values that will be entered into the meta-analysis. Although the p-curve archi- tects provide a set of selection criteria for which p values should be included (Simonsohn et al., 2014), they recognize that, as with any meta-analysis, ambiguous situations will require subjective judgments. Transparency for these judg- ments is achieved through two mechanisms—disclosure and secondary “Robustness Test” analyses. In terms of disclo- sure, a column in Table S2 in the online supplemental materials reports the decisions that were made in cases where the p-value selection was not obvious. In cases where there is a different value that, although not the primary choice, could have been alternatively included, this value is reported in the “Robustness Test” column. The Robustness Test is a second p curve, calculated alongside the main p curve, but with all the alternate p values replacing the primary ones (for those studies for which there are no alternate analyses, the primary analyses are retained). This second test provides confidence that the true p curve is robust to subjective decision rules.

When a single priming study had multiple DVs, including all these as separate p values would have overweighted the study in the overall p-curve analysis. As a result, following Simonsohn et al.’s (2014) recommendations, the first reported analysis was always included in the primary analy- sis. This occurred in five studies (Johnson, Rowatt, & LaBouff, 2012; LaBouff et al., 2012; Pichon & Saroglou, 2009; Ramsay, Pang, Shen, & Rowatt, 2014; Rodriguez, Neighbors, & Foster, 2013). In each case, an overall p value was calculated by combining all dependent measures to pro- vide a “representative” analysis of the overall effect. This value was entered into the Robustness Test.

Finally, when multiple conditions (e.g., religious, control, and “secular”; McCullough, Carter, DeWall, & Corrales, 2012) were included, extraneous conditions were dropped and the p value for the differences of means between the reli- gious condition and most neutral control condition was included in the p-curve analysis.

Method. Test results for each relevant analysis (see Table S2 in the online supplemental materials) were entered into the p-curve web application (http://www.p-curve.com/app/). Exact p values were recalculated to five decimal places from the original test values (e.g., t-test, chi-square) or, where available, the reported means and standard deviations. When calculating new test values, and when specific sample sizes for individual conditions were not reported, equal sizes were assumed. Once all values were entered, the web app calculated the p-curve skew. P values were winsorized at .01 and .99 to insulate the analysis from outliers (not winsorizing does not notably change results for either Analysis 3 or 5).

将每个相关分析的测试结果（见在线补充材料中的表S2）输入到p曲线的网络应用程序（http://www.p-curve.com/app/）。 从原始测试值（例如，t检验，卡方）重新计算精确的p值（保留五个小数位），或者从报告的平均值和标准偏差中计算。 当计算新的测试值时，没有报告单个条件的特定样本大小时，假设相等的大小。 一旦输入所有值，Web应用程序就会计算出p曲线偏态性。 P值在0.01和0.99之间进行了融合，以将分析与异常值隔离（不分析不会显着改变分析3或5的结果）。

Results and discussion. The resulting p curve was significantly right-skewed, χ2(134) = 201.98, p = .0001(Figure 3), with 45 of 67 p values lower than p = .025. The Robustness Test’s p curve was similarly right-skewed, χ2(136) = 230.05, p < .0001, with 43 of 68 p values lower than p = .025. These results suggest that the body of studies reflects a true effect of religious priming, and not an artifact of publication bias and p hacking. 所得到的p曲线呈显著右偏态，χ2（134）= 201.98，p = 0.0001（图3），67 个p值中有45个 p值低于0.025。 鲁棒性测试的p曲线类似于右偏，χ2（136）= 230.05，p <.0001，68 个p值中有43个 p值低于0.025。 这些结果表明，研究结果反映了「宗教启动」存在的真实的效应，而不是出版偏倚或者p hacking。

p-curve 评估总体效应量

[@simonsohn_p-curve_2014]不仅将其用于评估发表偏差p-hacking，还可以用来估计总体效应量。

Figure 5A shows the resulting p-curves. Both are right skewed, but Asian disease’s p-curve was more so. Whereas 83% of the Asian Disease Problem’s significant p values were below .01, only 31% of the Sunk Cost Fallacy’s significant p values were below .01. Figure 5B reports the resulting effect size estimates, comparing p-curve’s estimates to a naive estimate, computed by averaging the effect size observed across the significant studies, and an earnest estimate, computed by averaging the effect size across all studies, regardless of signifi- cance. Because these results were not p hacked, we can safely assume that the earnest estimate represents the best estimate of the true effect size. The bias of the naive estimate is small for the Asian disease problem, as a large proportion of those studies were significant. It estimates a true effect size of .66, whereas the average across all studies was .60. Reassuringly, p-curve’s estimate agrees with the earnest estimate, and thus corrects little when little needs to be corrected.

http://psych-your-mind.blogspot.jp/2012/02/friday-fun-one-researchers-p-curve.html

References